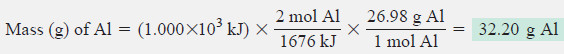Stoichiometry of Thermochemical Equation

– A thermochemical equation is a balanced equation that includes the heat of reaction (ΔH_rxn).

– Keep in mind that the ΔH_rxn value shown refers to the amounts (moles) of substances and their states of matter in that specific equation.

– The enthalpy change of any process has two aspects:

(1) Sign

– The sign of ΔH depends on whether the reaction is exothermic (-) or endothermic (+).

– A forward reaction has the opposite sign of the reverse reaction.

– Decomposition of 2 mol of water to its elements (endothermic):

2H₂O_(l) → 2H_2(g) + O_2(g) ΔH_rxn = 572 kJ

– Formation of 2 mol of water from its elements (exothermic):

2H_2(g) + O_2(g) → 2H₂O_(l) ΔH_rxn= -572 kJ

(2) Magnitude

– The magnitude of ΔH is proportional to the amount of substance reacting.

– Formation of 1 mol of water from its elements (half the amount in the preceding equation):

H_2(g) + 1/2 O_2(g) → H₂O_(l) ΔH_rxn= -286 kJ

– Note that, in thermochemical equations, we often use fractional coefficients to specify the magnitude of ΔH_rxn for a particular amount of substance.

– Moreover, in a particular reaction, a certain amount of substance is thermochemically equivalent to a certain quantity of energy.

– In the reaction just shown,

286 kJ is thermochemically equivalent to 1 mol of H_2(g)

and 286 kJ is thermochemically equivalent to mol of O_2(g)

286 kJ is thermochemically equivalent to 1 mol of H₂O_(l)

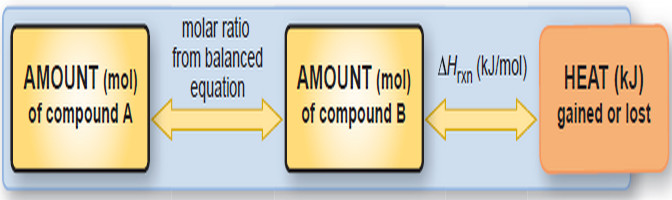
– Just as we use stoichiometrically equivalent molar ratios to find amounts of substances, we use thermochemically equivalent quantities to find the heat of reaction for a given amount of substance.

– Also, just as we use molar mass (in g/mol of substance) to convert moles of a substance to grams, we use the heat of reaction (in kJ/mol of substance) to convert moles of a substance to an equivalent quantity of heat (in kJ).

– The followingFigure shows this new relationship, and the following solved Problem applies it.

Solved problem

– Using the Heat of Reaction (ΔHrxn) to Find Amounts

The major source of aluminum in the world is bauxite (mostly aluminum oxide). Its thermal decomposition can be represented by:

Al₂O_3(s) → 2Al_(s) + 3/2 O_2(g) ΔH_rxn =1676 kJ

If aluminum is produced this way , how many grams of aluminum can form when 1.000×10³ kJ of heat is transferred?

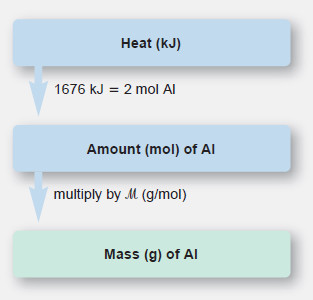
Plan:

– From the balanced equation and the enthalpy change, we see that 2 mol of Al forms when 1676 kJ of heat is absorbed.

– With this equivalent quantity, we convert the given kJ transferred to moles formed and then convert moles to grams.

Solution:

Combining steps to convert from heat transferred to mass of Al:

Check:

The mass of aluminum seems correct: ≈1700 kJ forms about 2 mol of Al (54 g), so 1000 kJ should form a bit more than half that amount (27 g).

Comment:

– In practice, aluminum is not obtained by heating but by supplying electrical energy.

– Because ΔH is a state function, however, the total energy required for this chemical change is the same no matter how it occurs.

Summary

– A thermochemical equation shows the balanced equation and its ΔH_rxn.

– The sign of ΔH for a forward reaction is opposite that for the reverse reaction.

– The magnitude of ΔH depends on the amount and physical state of the substance reacting and the ΔH per mole of substance.

– We use the thermochemically equivalent amounts of substance and heat from the balanced equation as conversion factors to find the quantity of heat when a given amount of substance reacts.

References

Principles of Inorganic Chemistry / Brian W. Pfennig / 1st ed, 2015 /John Wiley & Sons, Inc/ USA.
Principles of general Chemistry / Martin S. Silberberg / 2nd ed, 2010 /The McGraw-Hill Companies, Inc./ USA.
Inorganic Chemistry /Peter Atkins, Tina Overton, Jonathan Rourkel, Mark Weller, Fraser Armstrong, Mike Hagerman / 6th ed, 2014 /W. H. Freeman and Company/ New York, USA.
Complete Chemistry for Cambridge IGCSE RG Student book/RoseMarie Gallagher, Paul Ingram / 3rd ed, 2014 / Oxford University Press / USA.