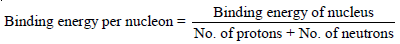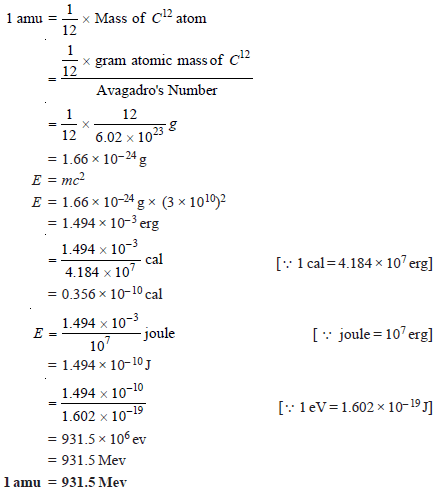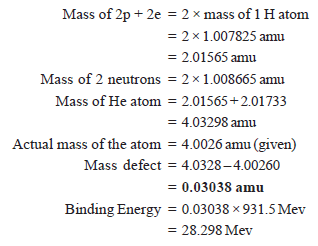Nuclear Binding Energy: Definition, Formula, Explanation
– In this subject, we will discuss Nuclear Binding Energy: (Definition, Formula, Explanation)
Nuclear Binding Energy
– The atomic nucleus is made of protons and neutrons closely packed in a small volume.
– Although there exist intensive repulsive forces between the component protons, the nucleus is not split apart. This is so because the nucleons are bound to one another by very powerful forces.
– The energy that binds the nucleons together in the nucleus is called the Nuclear binding energy.
– Nuclear binding energy is The energy that binds the nucleons together in the nucleus.
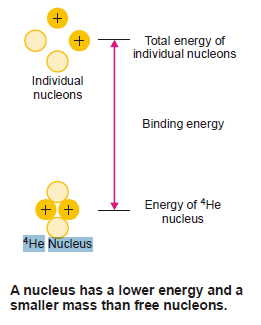
– When a nucleus is formed from individual protons and neutrons, there occurs a loss of mass (mass defect).
– According to Einstein’s theory, it is this mass defect that is converted into binding energy.
– Hence binding energy is the energy equivalent of the mass defect.
– The various nuclei have different binding energies.
– Binding energy is a measure of the force that holds the nucleons together.
– Hence an energy equivalent to the binding energy is required to disrupt a nucleus into its constituent protons and neutrons.
– Since nuclear energy is of an extremely high order, it is not easy to fission a nucleus.
Calculation of Binding Energy
– The binding energy of a nucleus can be calculated from its mass defect by using Einstein’s equation, ΔE = Δm × c2.
Solved Problem (1): What is the binding energy for 11B5 nucleus if its mass defect is 0.08181 amu?
Solution:
– Substituting values in Einstein’s equation,
– No. of nuclei in one mole is 6.02 × 1023 (Avogadro’s Law).
∴ The binding energy for the 11B5 nucleus, ΔE, may be expressed as:
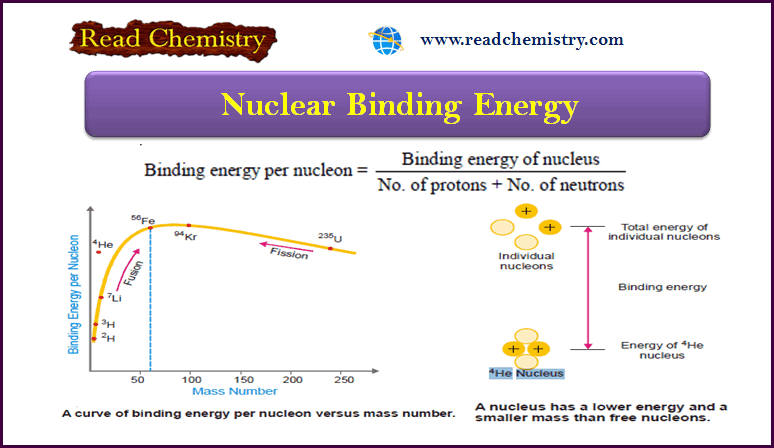
Binding energy per nucleon
– It can be calculated by dividing the total binding energy by the sum of the number of protons and neutrons present in the nucleus:
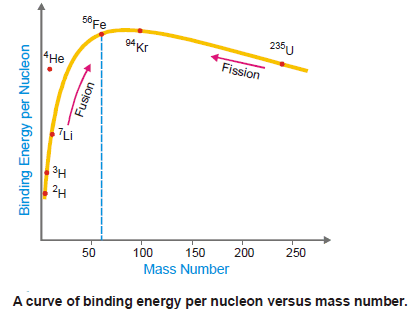
– By plotting the binding energy per nucleon against the mass number, we get the graph shown in the following Figure:
– The figure shows the relative stability of the various nuclei.
– The greater the binding energy per nucleon the more stable the nucleus.
– Thus the nuclei of about 60 atomic mass having maximum energy per nucleon are most stable e.g., 56Fe.
– The nuclei that are heavier or lighter than this have lower binding energies per nucleon and are less stable.
– Thus 235U undergoes fission into lighter and more stable isotopes such as 139Ba and 94Kr with the release of energy.
– Similarly, two or more lighter nuclei (2H, 3H) with lower binding energy per nucleon combine or fuse into a heavier and more stable nucleus.
– This is also accompanied by the release of energy.
Equivalence of amu and Energy
– Since 1 amu is exactly equal to1/12 th of the mass of C12 atom, therefore
Solved Problem (2): Calculate the binding energy per nucleon (in Mev) in He atom 42 He which has a mass of 4.00260 amu. Mass of an electron = 1.008655 amu and mass of 1 hydrogen atom = 1.007825 mass.
Solution:
– In a Helium atom, there are 2 electrons, 2 protons, and 2 neutrons.
1 amu = 931.5 Mev
Binding energy per nucleon: