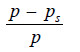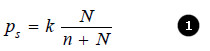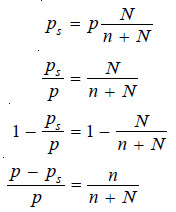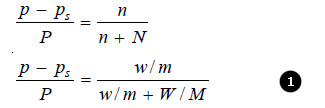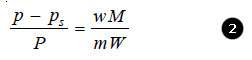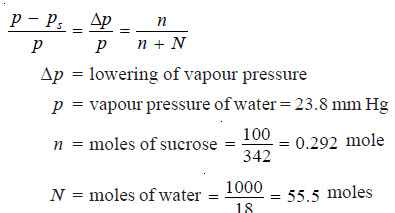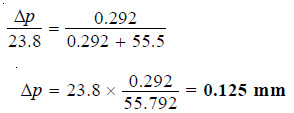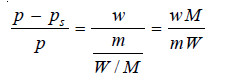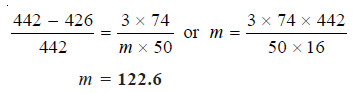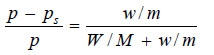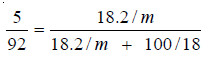Lowering of vapour pressure- Raoult’s law
In this subject we will restrict our discussion to Raoult’s Law
COLLIGATIVE PROPERTIES
– Dilute solutions containing non-volatile solute exhibit the following properties :
(1) Lowering of the Vapour Pressure
(2) Elevation of the Boiling Point
(3) Depression of the Freezing Point
(4) Osmotic Pressure
– The essential feature of these properties is that they depend only on the number of solute particles present in solution.
– Being closely related to each other through a common explanation, these have been grouped together under the class name Colligative Properties (Greek colligatus = Collected together).
– A colligative property may be defined as one which depends on the number of particles in solution and not in any way on the size or chemical nature of the particles.
– Consequent to the above definition, each colligative property is exactly related to any other. Thus if one property is measured, the other can be calculated.
– The colligative properties of dilute solutions are particularly important as these provide valuable methods for finding the molecular weights of the dissolved substances.
LOWERING OF VAPOUR PRESSURE : RAOULT’S LAW
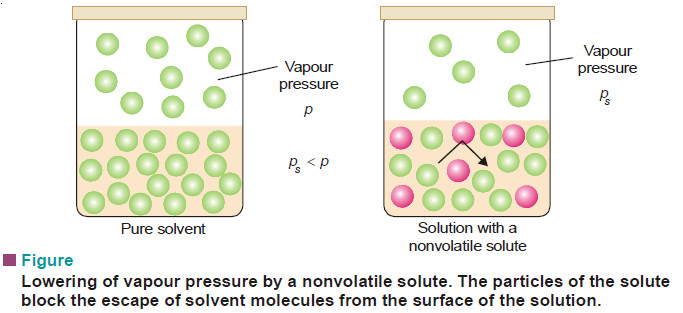
– The vapour pressure of a pure solvent is decreased when a non-volatile solute is dissolved in it.
– If (p) is the vapour pressure of the solvent and (ps) that of the solution, the lowering of vapour pressure is (p – ps).
– This lowering of vapour pressure relative to the vapour pressure of the pure solvent is termed the Relative lowering of Vapour pressure.
Thus,
Relative Lowering of Vapour Pressure =
– As a result of extensive experimentation, Raoult (1886) gave an empirical relation connecting the relative lowering of vapour pressure and the concentration of the solute in solution. This is now referred to as the Raoult’s Law.
– It states that : the relative lowering of the vapour pressure of a dilute solution is equal to the mole fraction of the solute present in dilute solution.
Raoult’s Law can be expressed mathematically in the form :
where:
n = number of moles or molecules of solute
N = number of moles or molecules of solvent.
Derivation of Raoult’s Law
The vapour pressure of the pure solvent is caused by the number of molecules evaporating from its surface. When a nonvolatile solute is dissolved in solution, the presence of solute molecules in the surface blocks a fraction of the surface where no evaporation can take place.
This causes the lowering of the vapour pressure. The vapour pressure of the solution is, therefore, determined by the number of molecules of the solvent present at any time in the surface which is proportional to the mole fraction. That is,
where N = moles of solvent and n = moles of solute.
(k) being proportionality factor
In case of pure solvent n = 0 and hence
Now from equation (1), the vapour pressure p = k
Therefore the equation (1) assumes the form:
This is Raoult’s Law.
Ideal Solutions and Deviations from Raoult’s Law
A solution which obeys Raoult’s law strictly is called an Ideal solution. A solution which shows deviations from Raoult’s law is called a Nonideal or Real solution.
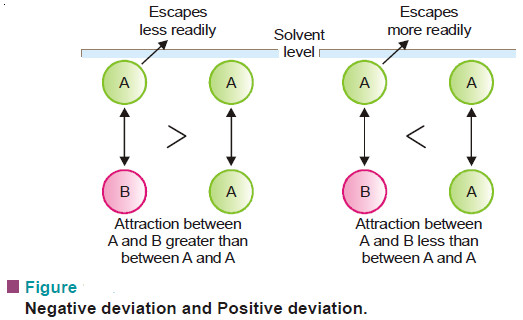
Suppose the molecules of the solvent and solute are represented by (A)and (B) respectively. Now let γAB be the attractive force between (A) and (B), and γAA between (A) and (A). If
γAB = γAA
The solution will show the same vapour pressure as predicted by Raoult’s law and it is an ideal solution. However, if
γAB > γAA
molecule A will escape less readily and the vapour pressure will be less than that predicted by Raoult’s law (Negative deviation).
On the other hand, if
γAB < γAA
A molecule will escape from the solution surface more readily and the vapour pressure of the solution will be higher than predicted by Raoult’s law (Positive deviation).
In very dilute solutions of nonelectrolytes, the solvent and solute molecules are very much alike in both molecular size and molecular attractions. Thus such solutions tend to approach the ideal behaviour and obey Raoult’s law fairly accurately.
Determination of Molecular Mass from Vapour Pressure Lowering
The molecular mass of a nonvolatile solute can be determined by measuring the lowering of vapour pressure (p – ps) produced by dissolving a known weight of it in a known weight of the solvent.
If in a determination w grams of solute is dissolved in W grams of the solvent, m and M are molecular masses of the solute and solvent respectively, we have :
No. of Moles of solute (n) = w/m
No. of Moles of solvent (N) = W/M
Substituting these values in the Raoult’s law Equation,
Since for very dilute solution, the number of moles (molecules) of solute (w/m), is very small, it can be neglected in the denominator. The equation (1) can now be written as:
Knowing the experimental value of p – ps/p, and the molecular mass of the solvent (M), the molecular weight of solute (m) can be calculated from (1) or (2)
SOLVED PROBLEMS ON RAOULT’S LAW
Problem(1):
Calculate the vapour pressure lowering caused by the addition of 100 g of sucrose (mol mass = 342) to 1000 g of water if the vapour pressure of pure water at 25°C is 23.8 mm Hg.
solution:
Using Raoult’s Law Equation
Substituting values in equation (1):
Thus the lowering of vapour pressure = 0.125 mm Hg
Problem(2):
The vapour pressure of ether (mol mass = 74) is 442 mm Hg at 293 K. If 3g of a compound A are dissolved in 50 g of ether at this temperature, the vapour pressure falls to 426 mm Hg. Calculate the molecular mass of A. Assume that the solution of A in ether is very dilute.
solution:
Here the approximate form of the Raoult’s law Equation will be used.
In this case :
w, the mass of solute (A) = 3 g
W, the mass of solvent (ether) = 50 g
m, the mol mass of solute A = ?
M, the mol mass of solvent (ether) = 74
p, the vapour pressure of solvent (ether) = 442 mm
ps, the vapour pressure of solution = 426 mm
Substituting the values in equation above,
Thus the molecular weight of A is 123
Problem(3):
2. 18.2 g of urea is dissolved in 100 g of water at 50°C. The lowering of vapour pressure produced is 5 mm Hg. Calculate the molecular mass of urea. The vapour pressure of water at 50°C is 92 mm Hg.
solution:
Since the solution is not very dilute, the complete Raoult’s Law Equation applied is:
In this case :
w, the mass of solute (urea) = 18.2 g
W, the mass of solvent (water) = 100 g
m, the mol mass of solute (urea) = ?
M, the mol mass of solvent (water) = 18
p – ps, the lowering of vapour pressure = 5 mm
p, the vapour pressure of solvent (water) = 92 mm
Substituting these values in equation above,
Hence m, the molecular mass of urea = 57.05