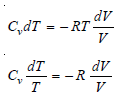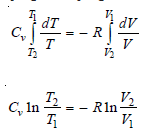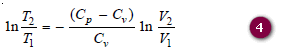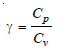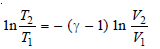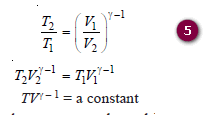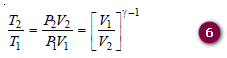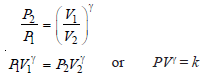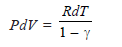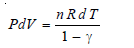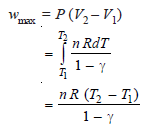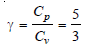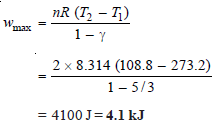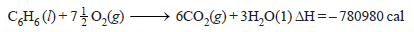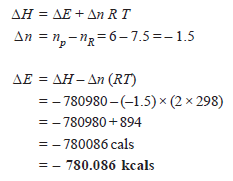Read Chemistry
Adiabatic Expansion of an Ideal Gas
– A process carried in a vessel whose walls are perfectly insulated so that no heat can pass through them, is said to be adiabatic.
– In the adiabatic process there is no heat exchange between a system and surroundings, and q = 0.
– According to the First law:
ΔE = q – w = 0 – w
ΔE = – w …(1)
– Since the work is done at the expense of internal energy, the internal energy decreases and the temperature falls.
– Consider 1 mole of an ideal gas at pressure P and a volume V.
– For an infinitesimal increase in volume dV at pressure P, the work done by the gas is –PdV.
– The internal energy decreases by dE.
– According to equation (1):
dE = – PdV …(2)
– By definition of molar heat capacity at constant volume:
dE = CvdT …(3)
– From (2) and (3):
CvdT = – PdV
– For an ideal gas:
P = RT/V
– and hence:
– Integrating between T1, T2 and V1, V2 and considering Cv to be constant:
– Since R = Cp – Cv , this equation may be written as:
– Replacing – ve sign by inverting V2/V1 to V1/V2and taking antilogarithms:
– We can also eliminate the temperature by making use of the ideal gas relationship:
– Equating the right-hand sides of equations (5) and (6):
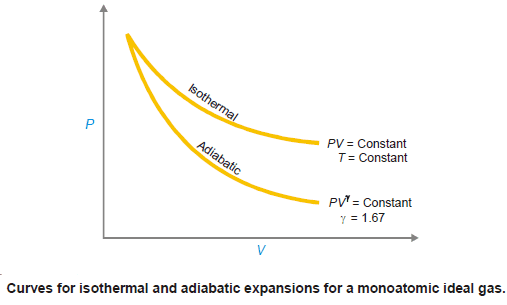
Comparison between Isothermal and Adiabatic Expansions
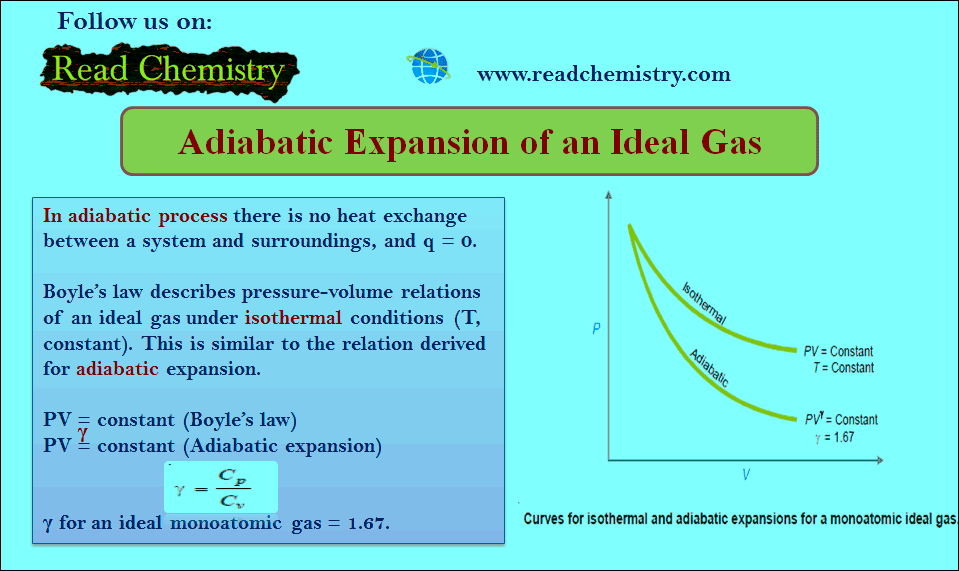
– Boyle’s law describes the pressure-volume relations of an ideal gas under isothermal conditions (T, constant).
– This is similar to the relation derived for adiabatic expansion.
PV = constant (Boyle’s law)
PVγ= constant (Adiabatic expansion)
– γ for an ideal monoatomic gas = 1.67.
– The difference between the two processes is in an isothermal process, the temperature of a system remains constant while in an adiabatic process, the temperature must change.
Explanation:
– In an isothermal process, heat is absorbed to make up for the work done by the gas in expansion and the temperature remains unchanged.
– On the other hand, adiabatic expansion takes place at the expense of internal energy which decreases and the temperature falls.
– For the same reason, the curve for the adiabatic process is steeper than that for the isothermal process.
Work done In adiabatic Reversible Expansion
Step (1): Value of VdP from adiabatic equation
– For an adiabatic process:
PVγ= constant
– Differentiating it, we have:
γ PVγ – 1 dV + Vγ dp = 0
– Dividing by V γ – 1, we get:
γ PdV + VdP = 0
VdP = – γ PdV …(1)
Step (2): Value of VdP from the ideal gas equation
– For 1 mole of an ideal gas:
PV = RT
– Complete differentiation gives:
PdV + VdP = RdT
VdP = RdT – PdV …(2)
Step (3): Substitution
– Substituting the value of VdP from (1) in (2) we get:
RdT – PdV = – γ PdV
RdT = P (1 – γ) dV
– If there are n moles of a gas:
Step (4): Integration
– Integrating from T1, V1 to T2, V2with γ constant:
– When T2 > T1, wmax is negative because 1 – γ is negative. This means that work is done on the gas.
– On the other hand, when T2 < T1, wmax is positive which means that work is done by the gas.
Solved Problem
Problem (1): Calculate w for the adiabatic reversible expansion of 2 moles of an ideal gas at 273.2 K and 20 atm to a final pressure of 2 atm.
Solution:
Given:
Cp = 5R/2, mole–1deg–1
Cv = 3R/2, mole–1deg–1
R = 8.314J mole–1deg–1
Step 1: To calculate the value of T2, the final temperature, using the equation:
(T2/ T1)γ = (P2 / P1)γ –1
Substituting the value of γ in (1):
(T2/ 273.2)5/3 = (2 / 20)
Solving it, we get:
T2= 108.8 K
Step 2: To calculate maximum work under adiabatic conditions:
The work done under adiabatic conditions may be obtained by calculating decrease in internal Energy:
w = – ΔE = – nCv (T2 – T1)
= – 2 × 3 / 2 × 8.314 (108.8 – 273.2)
= 4100 J = 4.1 kJ
Problem (2): At 25ºC for the combustion of 1 mole of liquid benzene the heat of reaction at constant pressure is given by:
What would be the heat of reaction at constant volume?
Solution:
We have:
Reference: Essentials of Physical Chemistry /Arun Bahl, B.S Bahl and G.D. Tuli / multicolour edition.
