Viscosity – Measurement of Viscosity
Viscosity
– Viscosity is the resistance of a liquid to flow.
– A liquid may be considered to be consisting of molecular layers arranged one over the other.
– When a shearing force is applied to a liquid, it flows. However, the forces of friction between the layers offer resistance to this flow.
– It is a measure of its frictional resistance.
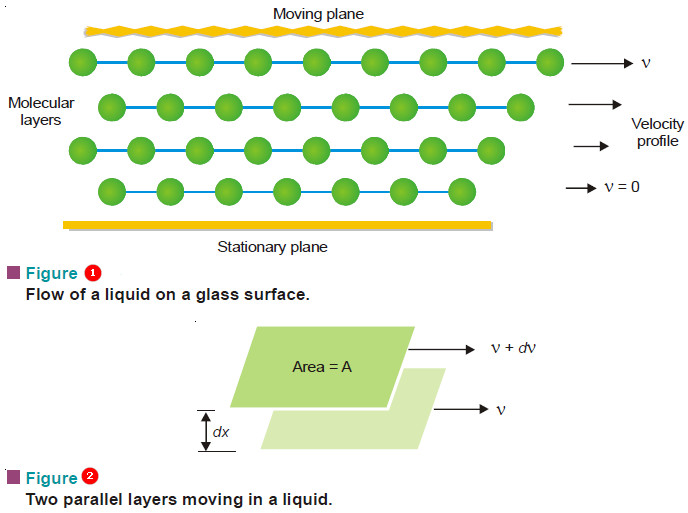
– Let us examine a liquid flowing on a glass surface (Fig. 1). The molecular layer in contact with the stationary surface has zero velocity. The successive layers above it move with increasingly higher velocities in the direction of the flow.
– Now consider two adjacent moving layers of a liquid (Fig. 2).
– Let these be separated by a distance (dx) and have a velocity difference (dv).
– The force of friction (F) resisting the relative motion of the two layers is directly proportional to the area (A) and the velocity difference (dv), while it is inversely proportional to the distance between the layers.
That is,
where (η) (Greek letter eta) is the proportionality constant. It is known as the Coefficient of Viscosity or simply viscosity of a liquid.
– Coefficient of Viscosity (η) has a specific value for a given liquid at the same temperature. It may be defined from equation (2) as : the force of resistance per unit area which will maintain unit velocity difference between two layers of a liquid at a unit distance from each other.
– The reciprocal of viscosity is called Fluidity and is denoted by φ.
Units of Viscosity
– The dimensions of the coefficient of viscosity ( η ) may be derived from equation (2).
– Thus in CGS system the unit of (η) is expressed as g cm–1 s–1. It is called poise (P).
– In practice smaller units centipoise (10–2 poise) and millipoise (10–3 poise) are used.
– The SI unit is kg m–1 s–1. One poise is equal to one-tenth of the SI unit i.e.
1 poise = 1 g cm–1 s–1 = 0.1 kg m–1 s–1
Measurement of Viscosity – The Ostwald Method
– Viscosity of a liquid can be determined with the help of Pioseulle’s equation.
– This expression which governs the flow of a liquid through a capillary may be written as:
where
V = the volume of the liquid flowing through capillary in time t,
P = the pressure-head,
r = the radius of the tube and l its length.
– The experimental measurement of (P) , (r) , ( l) and (V) offers considerable difficulty. Therefore, it is not possible to find the absolute coefficient of viscosity (η) straight away from Poiseulle’s equation.
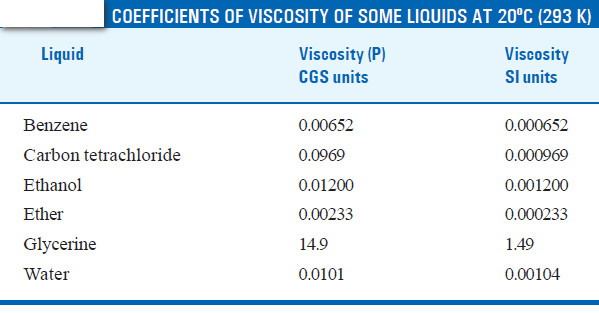
– Ordinarily, the viscosity of a liquid is determined with respect to that of water. This is called Relative Viscosity. Let (t1) and (t2) be the times of flow of a fixed volume (V) of the two liquids through the same capillary.
– The expression for relative viscosity ( η1/ η2) can be derived from equation (1).
– Since the pressure-head is proportional to density (d) of the liquid, from (2) we have:
– Substituting the value of the viscosity coefficient of water (η2) in (3), we can find the absolute viscosity of the given liquid (η1).
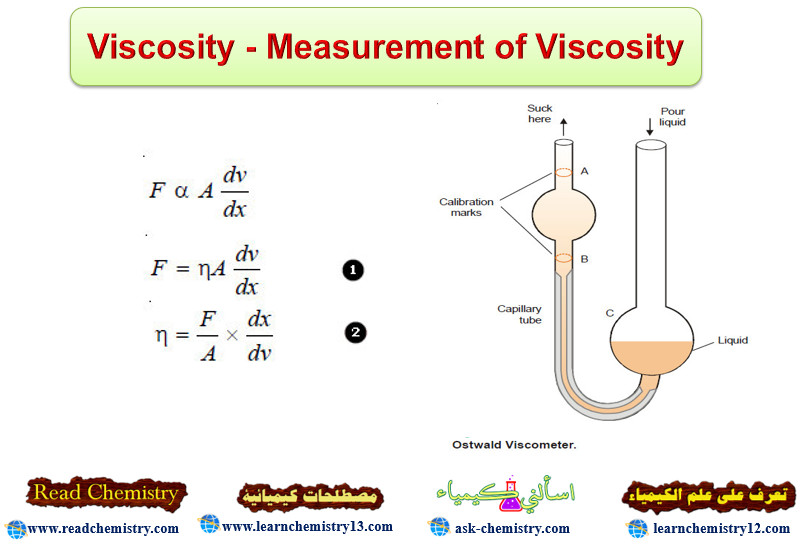
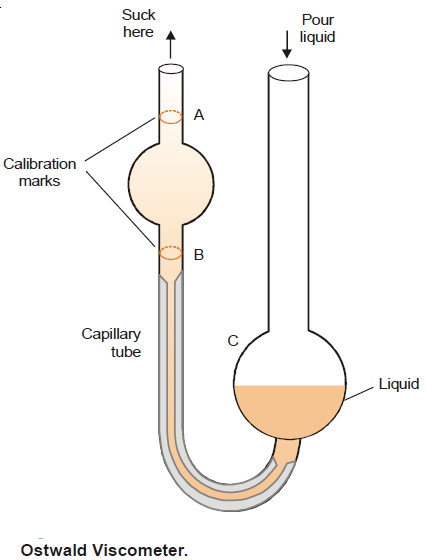
Ostwald Viscometer
– The apparatus commonly used for the determination of relative viscosity of a liquid is known as Ostwald viscosimeter or viscometer.
– A simple form of it is shown in the following Figure. The left-hand limb is essentially a pipette with two calibration marks A and B. A length of capillary tube joins the pipette to a bulb C in the right-hand limb.
– A definite volume of liquid (say 25 ml) is poured into the bulb C with a pipette.
– The liquid is sucked up near to the top of the left-limb with the help of a rubber tubing attached to it.
– The liquid is then released to flow back into the bulb C. The time (t1) from A to B is noted with a stopwatch. Then the apparatus is cleaned and the experiment repeated with water, taking about the same volume.
– The time of flow of water (t2) from A to B is recorded. The density of the liquid (d) and water (dw) are determined with the help of a pyknometer.
– The relative viscosity coefficient is calculated from the expression:
– Knowing the value of the viscosity coefficient of water (ηw) at the temperature of the experiment, the absolute viscosity coefficient (η) of the given liquid can be found.
Solved Problem on viscosity
SOLVED PROBLEM (1): In an experiment with Ostwald viscometer, the times of flow of water and ethanol are 80 sec and 175 sec at 20ºC. The density of water = 0.998 g/cm3 and that of ethanol = 0.790 g/cm3. The viscosity of water at 20ºC is 0.01008 poise. Calculate the viscosity of ethanol.
SOLUTION:
SOLVED PROBLEM (2): In an experiment with Ostwald viscometer, pure water took 1.52 minutes to flow through the capillary at 20ºC. For the same volume of another liquid of density 0.80 g cm–3 the flow time was 2.25 minutes. Find the relative viscosity of the liquid and its absolute viscosity in centipoise. Density of water at 20ºC is 0.9982 and absolute viscosity of water is 1.005 centipoise.
SOLUTION:
Effect of temperature on viscosity of a liquid
– In general, the (η) decreases with increase in temperature. The variation of (η) with temperature can be expressed by the following relationship:
where A and E are constants.
– Taking logarithms on both sides, we get
comparing equation (2) with:
y = mx + c (equation of straight line)
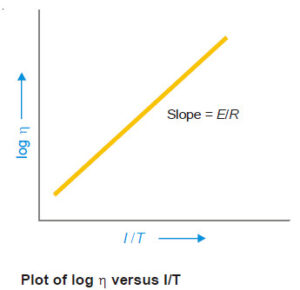
A plot of (log η) versus (1/T) should be a straight line. It has been verified for a variety of liquids.
It has also been found that there is 2% decrease in viscosity for every increase in one degree of temperature of the liquid.

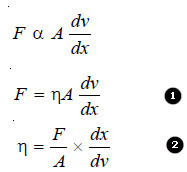
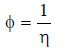
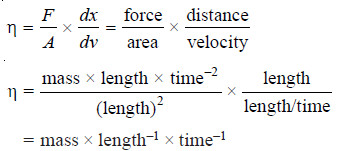
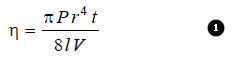
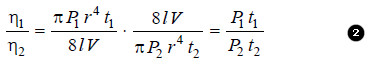
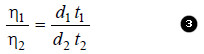
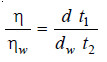
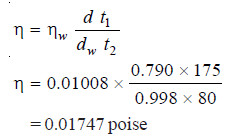
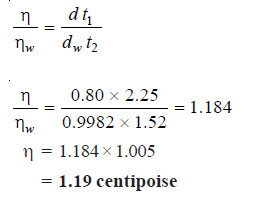
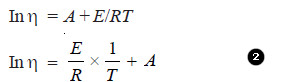




Could you send me these note . Thanks now.
جميل