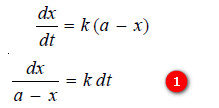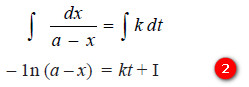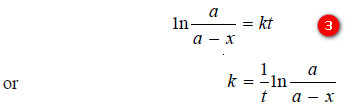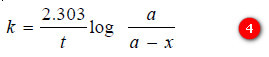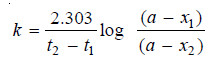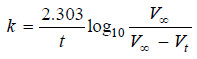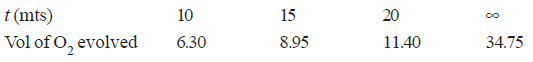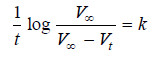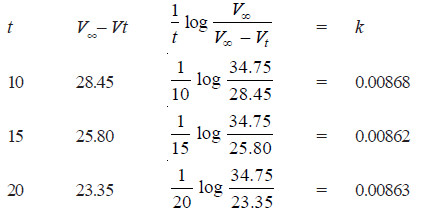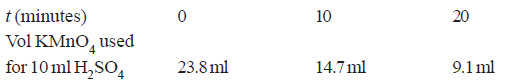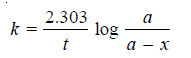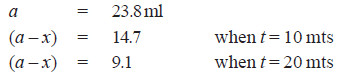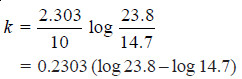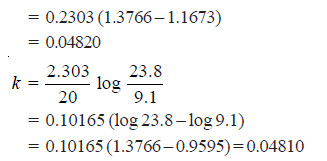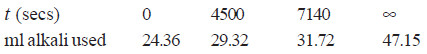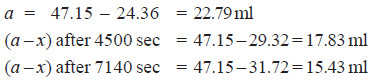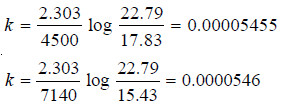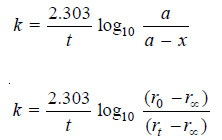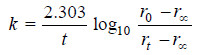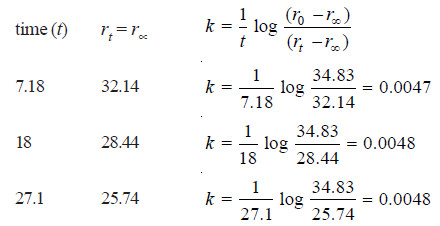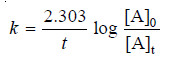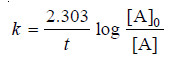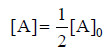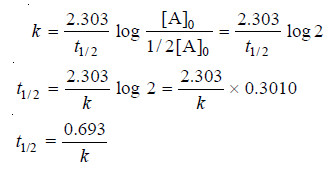First Order Reaction -Examples and Solved problems

First order reaction

– Let us consider a first order reaction:

A → products

– Suppose that at the beginning of the reaction (t = 0), the concentration of A is a moles liter^–1.

– If after time t, x moles of A have changed, the concentration of A is a – x.

– We know that for a first-order reaction, the rate of reaction, dx/dt, is directly proportional to the concentration of the reactant. Thus,

– Integration of the expression (1) gives:

– where (I) is the constant of integration.

– The constant k may be evaluated by putting t = 0 and x = 0. Thus,

I = – ln a

– Substituting for (I) in equation (2):

– Changing into common logarithms:

– The value of k can be found by substituting the values of a and (a  – x) determined experimentally at time interval t during the course of the reaction.

– Sometimes the integrated rate law in the following form is also used:

where x₁ and x₂ are the amounts decomposed at time intervals t₁ and t₂ respectively from the start.

Examples of First order reactions

Some common reactions which follow first order kinetics are listed below :

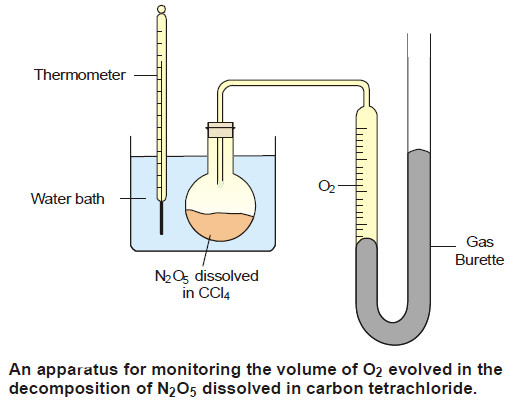
(1) Decomposition of N₂O₅ in CCl₄ solution

– Nitrogen pentoxide in carbon tetrachloride solution decomposes to form oxygen gas,

N₂O₅ → 2NO₂ + 1/2 O₂

– The reaction is carried out in an apparatus shown in the following Figure:

– The progress of the reaction is monitored by measuring the volume of oxygen evolved from time to time.

– If V_t be the volume of O₂ at any time t and V_∞ the final volume of oxygen when the reaction is completed, the V_∞ is a measure of the initial concentration of N₂O₅ and (V_∞ – V_t) is a measure of undecomposed N₂O₅ (a – x) remaining at time t. Thus,

– On substituting values of V_∞ , (V_∞ – V_t) at different time intervals, t, the value of k is found to be constant. Thus it is a reaction of the first order.

Solved Problem (1): From the following data for the decomposition of N₂O₅ in CCl₄ solution at 48°C, show that the reaction is of the first order

Solution:

– For a first order reaction, the integrated rate equation is:

– In this example, V_∞ = 34.75

Since the value of k is fairly constant, it is a first order reaction.

(2) Decomposition of H₂O₂ in aqueous solution

– The decomposition of H₂O₂ in the presence of Pt as catalyst is a first order reaction.

– The progress of the reaction is followed by titrating equal volumes of the reaction mixture against standard KMnO₄ solution at different time intervals.

Solved Problem (2):  A solution of H₂O₂ when titrated against KMnO₄ solution at different time intervals gave the following results :

Show that the decomposition of H₂O₂ is a first order reaction.

Solution:

– The integrated rate equation for first order reaction is

Since the volume of KMnO₄ used in the titration is the measure of the concentration of H₂O₂ in the solution

– Substituting these values in the rate equation above, we have;

– Since the value of k is almost constant, the decomposition of H₂O₂ is a first order reaction.

(3) Hydrolysis of an Ester

– The hydrolysis of ethyl acetate or methyl acetate in the presence of a mineral acid as catalyst, is a first order reaction.

CH₃COOC₂H₅ + H₂O → CH₃COOH + C₂H₅OH

– For studying the kinetics of the reaction, a known volume of ethyl acetate is mixed with a relatively large quantity of acid solution, say N/2 HCl.

– At various intervals of time, a known volume of the reaction mixture is titrated against a standard alkali solution.

– Hydrolysis of the ester produces acetic acid.

– Therefore as the reaction proceeds, the volume of alkali required for titration goes on increasing.

Solved Problem (3): The following data was obtained on hydrolysis of methyl acetate at 25°C in 0.35N hydrochloric acid. Establish that it is a first order reaction.

Solution:

– For a first order reaction:

– At any time, the volume of alkali used is needed for the acid present as catalyst and the acid produced by hydrolysis.

– The volume of alkali used for total change from t₀ to t_∝ gives the initial concentration of ester. Thus,

– Substituting values in the rate equation above, we have:

Since the values of k in the two experiments are fairly constant, the reaction is of the first order.

(4) Inversion of Cane sugar (sucrose).

– The inversion of cane sugar or sucrose catalyzed with dil HCl to give D-glucose and D-fructose follows the first order kinetics

C₁₂H₂₂O₁₁ +H₂O ⎯⎯→ C₆H₁₂O₆ + C₆H₁₂O₆

– The progress of the reaction is followed by noting the optical rotation of the reaction mixture with the help of a polarimeter at different time intervals.

– The optical rotation goes on changing since D-glucose rotates the plane of polarised light to the right and D-fructose to the left.

– The change in rotation is proportional to the amount of sugar decomposed.

– Let the final rotation be r_∞, the initial rotation t₀ while the rotation at any time t is r_t

The initial concentration, a is ∞ ( t₀ – r_∝).

The concentration at time t, (a – x) is ∝ (r_t – r_∝)

– Substituting in the first order rate equation,

– If the experimental values of t ( t₀ – r_∝) and (r_t – r_∝) are substituted in the above equation, a constant value of k is obtained.

Solved Problem (4): The optical rotation of sucrose in 0.9N HCl at various time intervals is given in the table below.

Show that inversion of sucrose is a first order reaction.

Solution:

– The available data is substituted in the first order rate equation for different time intervals

r₀ – r_∝ = 24.09 – (– 10.74) = 34.83 for all time intervals. Thus, the value of rate constant can be found.

Since the value of k comes out to be constant, the inversion of sucrose is a first order reaction.

Units of First order Rate constant

The rate constant of a first order reaction is given by:

– Thus the rate constant for the first order reaction is independent of the concentration.

– It has the unit time^–1

Calculation of Half-life of a First order Reaction

– Reaction rates can also be expressed in terms of half-life or half-life period.

– It is defined as the time required for the concentration of a reactant to decrease to half its initial value.

– In other words, half-life is the time required for one-half of the reaction to be completed.

– It is represented by the symbol t_1/2 or t_0.5.

– The integrated rate equation (4) for a first order reaction can be stated as :

where [A]₀ is initial concentration and [A] is concentration at any time t. Half-life, t_1/2, is time when initial concentration reduces to 1/2 i.e., 

Substituting values in the integrated rate equation, we have:

It is clear from this relation that :

(1) The half-life for a first order reaction is independent of the initial concentration.

(2) it is inversely proportional to k, the rate-constant.