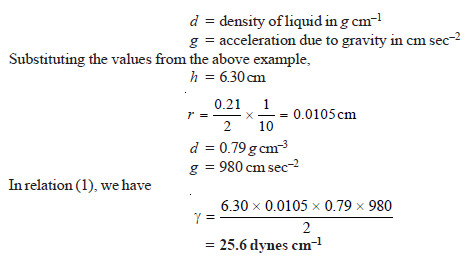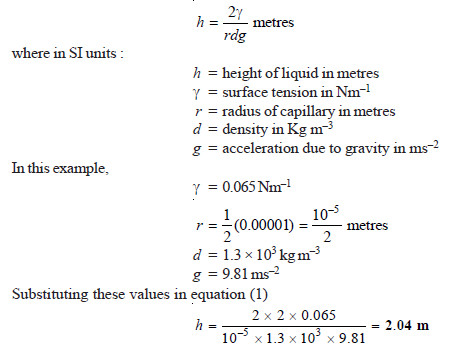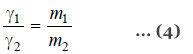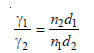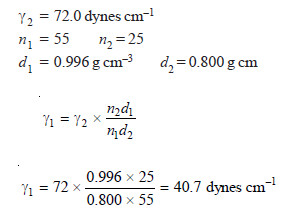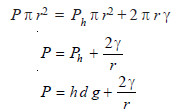Determination of Surface Tension
Surface Tension
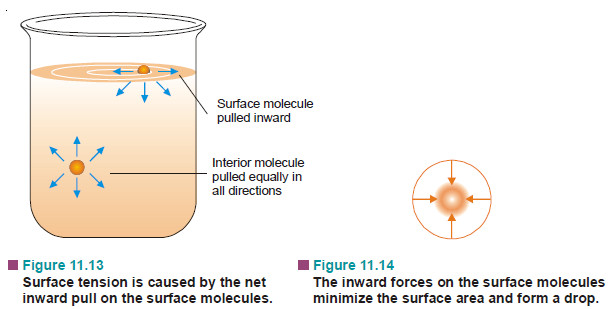
– Surface Tension property of liquids arises from the intermolecular forces of attraction.
– A molecule in the interior of a liquid is attracted equally in all directions by the molecules around it.
– A molecule in the surface of a liquid is attracted only sideways and toward the interior.
– The forces on the sides being counterbalanced the surface molecule is pulled only inward the liquid.
– Thus there is a tendency on the part of the surface molecules to go into the bulk of the liquid.
– The liquid surface is, therefore, under tension and tends to contract to the smallest possible area in order to have the minimum number of molecules at the surface. It is for this reason that in air, drops of a liquid assume spherical shapes because for a given volume a sphere has the minimum surface area.
– The surface tension (γ) is defined as: the force in dynes acting along the surface of a liquid at right angle to any line 1 cm in length.
Units of Surface Tension
– As included in the above definition the unit of surface tension in CGS system is dynes per centimetre (dyne cm–1).
– In SI system, the unit is Newton per metre (Nm–1). Both these units are related as : 1 dyne cm–1 = 1 m Nm–1
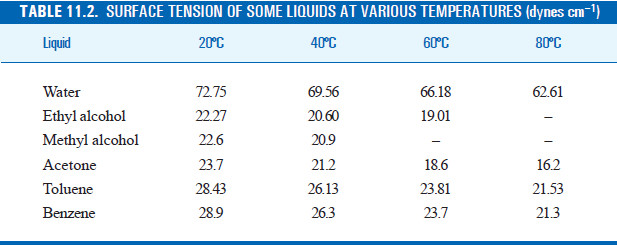
Effect of Temperature on Surface Tension
– A change in temperature causes a change in surface tension of a liquid.
– When temperature increases, there is an increase in kinetic energy of liquid molecules (KE ∝ T), thereby decreasing intermolecular forces. It results in decrease in the inward pull functioning on the surface of the liquid.
– In other words, surface tension decreases with increase in temperature. W. Ramsay and J. Shields gave the following relationship between surface tension of a liquid and its temperature
γ (M/ρ)2/3 = k (tc – t – 6)
where:
(k) = a constant (temperature coefficient),
(tc) = critical temperature and (t) any other temperature,
(M/ρ)2/3 represents molar surface energy of the liquid.
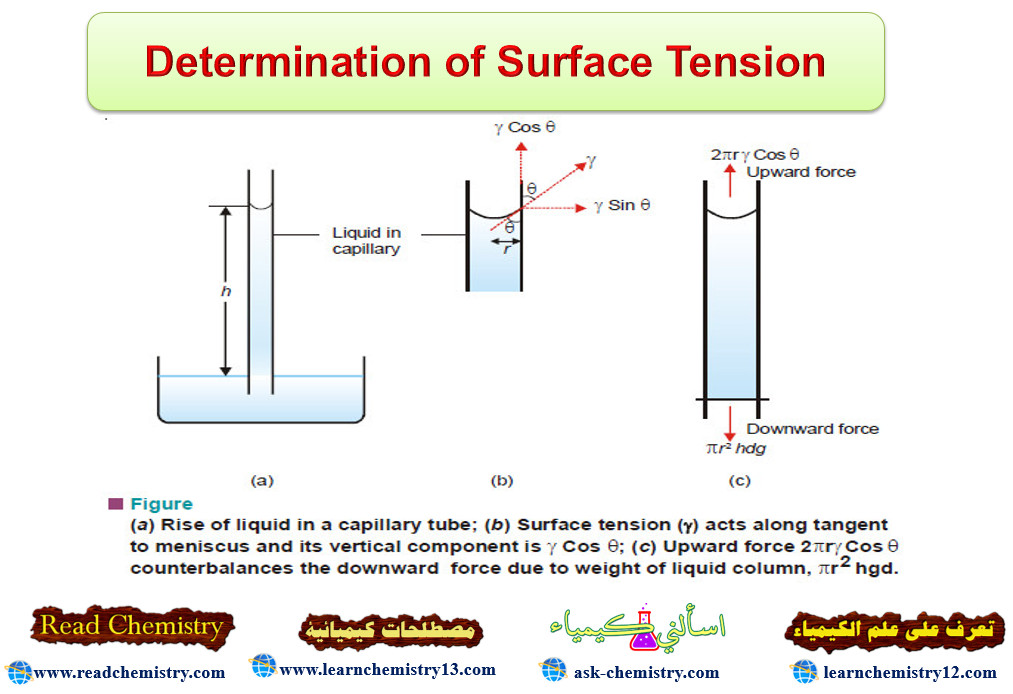
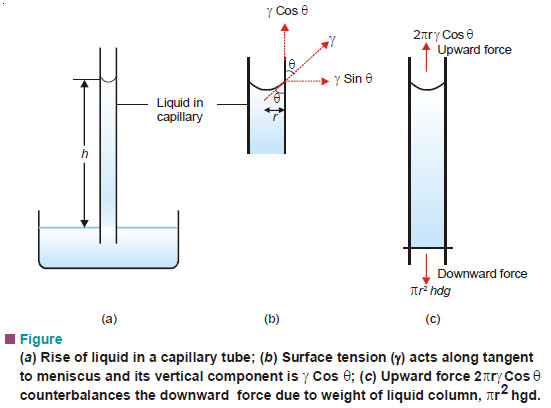
Determination of Surface Tension
The methods commonly employed for the determination of surface tension are :
(1) Capillary-rise Method
– A capillary tube of radius (r) is vertically inserted into a liquid. The liquid rises to a height (h) and forms a concave meniscus. The surface tension (γ) acting along the inner circumference of the tube exactly supports the weight of the liquid column.
– By definition, surface tension is force per 1 cm acting at a tangent to the meniscus surface. If the angle between the tangent and the tube wall is (θ) , the vertical component of surface tension is (γ cos θ).
– The total surface tension along the circular contact line of meniscus is (2πr) times. Therefore,
Upward force = 2πrγ cos θ
where (r) is the radius of the capillary.
– For most liquids, (θ) is essentially zero, and (cos θ = 1). Then the upward force reduces to (2πrγ).
– The downward force on the liquid column is due to its weight which is mass × gravity. Thus,
Downward force = hπr2 dg
where (d) is the density of the liquid.
But
Upward force = Downward force
2πrγ = hπr2 dg
In order to know the value of (γ), the value of (h) is found with the help of a travelling microscope and density (d) with a pyknometer.
SOLVED PROBLEM (1). A capillary tube of internal diameter 0.21 mm is dipped into a liquid whose density is 0.79 g cm–3. The liquid rises in this capillary to a height of 6.30 cm. Calculate the surface tension of the liquid. (g = 980 cm sec–2)
SOLUTION
Thus the surface tension of the given liquid is 25.6 dynes cm–1.
SOLVED PROBLEM (2): How high will sap rise in a plant if the capillaries are 0.01 mm diameter, the density of the fluid is 1.3 g cm–1 and its surface tension 0.065 Nm–1. (g = 981 cm s–2)
SOLUTION
Therefore in a plant with capillaries of 0.01 mm diameter, the sap will rise to a height of 2.04 metres.
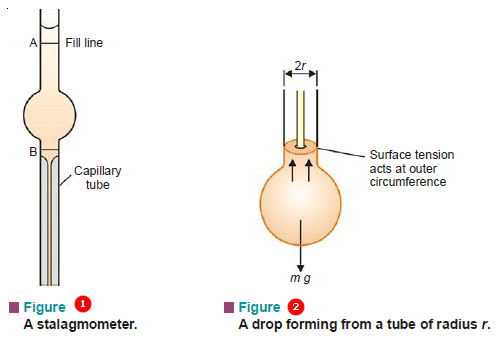
(2) Drop Formation Method
A drop of liquid is allowed to form at the lower end of a capillary tube (Fig. 2). The drop is supported by the upward force of surface tension acting at the outer circumference of the tube. The weight of the drop (mg) pulls it downward. When the two forces are balanced, the drop breaks. Thus at the point of breaking,
m g = 2 π r γ …(1)
m = mass of the drop
g = acceleration due to gravity
r = outer radius of the tube
The apparatus employed is a glass pipette with a capillary at the lower part. This is called a Stalagmometer or Drop pipette (Fig. 1). It is cleaned, dried and filled with the experimental liquid, say upto mark A. Then the surface tension is determined by one of the two methods given below.
(a) Drop-weight Method.
About 20 drops of the given liquid are received from the drop-pipette in a weighing bottle and weighed. Thus weight of one drop is found. The drop-pipette is again cleaned and dried. It is filled with a second reference liquid (say water) and weight of one drop determined as before
Then from equation (1)
m1 g = 2 π r γ1 …(2)
m2 g = 2 π r γ2 …(3)
Dividing (2) by (3)
Knowing the surface tension of reference liquid from Tables, that of the liquid under study can be found.
(b) Drop-number Method.
The drop-pipette is filled upto the mark A with the experimental liquid (No. 1). The number of drops is counted as the meniscus travels from A to B. Similarly, the pipette is filled with the reference liquid (No. 2) as the meniscus passes from A to B. Let (n1) and (n2) be the number of drops produced by the same volume (V) of the two liquids. Thus,
The volume of one drop of liquid (1) = V/n1
The mass of one drop of liquid (1) = (V/n1)d1
where d1 is the density of liquid (1).
Similarly,
The mass of one drop of liquid (2) = (V/n2)d2
Then from equation (4)
The value of d1 is determined with a pyknometer. Knowing d2 and γ2 from reference tables, γ1 can be calculated.
SOLVED PROBLEM. In the determination of surface tension of a liquid by the drop-number method, it gives 55 drops while water gave 25 drops for the same volume. The densities of the liquid and water are 0.996 and 0.800 g/cm3 respectively. Find the surface tension of the liquid if that of water is 72.0 dynes/cm.
SOLUTION
where:
γ1 = surface tension of liquid;
γ2 = surface tension of water;
n1 = number of drops of liquid;
n2 = number of drops of water.
Therefore, the surface tension of the given liquid is 40.7 dynes cm–1.
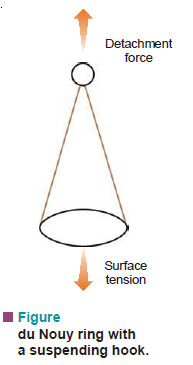
(3) Ring-detachment Method
– In this method the force required to detach a platinum ring (du Nouy ring) from the liquid surface
is measured.
– This force (F) is exactly equal to the downward pull due to surface tension γ acting along the circumference of the ring.
– Twice the length of the circumference (2 × 2πr) is taken since the liquid is in contact with both the inside and the outside of ring.
Thus,
F = 4 π r γ
or
where (r) is the radius of the ring.
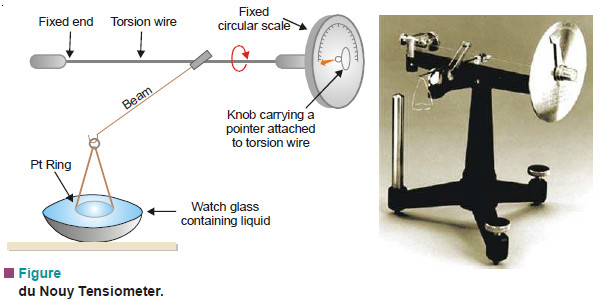
– The apparatus employed is called the du Nouy Tensiometer. Its essential parts are shown in the following Figure.
– One end of the torsion wire is fixed while the other is attached to a knob carrying a pointer. The pointer moves on a fixed scale. The scale is previously calibrated by taking different weights on the beam and noting the scale reading when it is lifted from the horizontal position.
– The liquid whose surface tension is to be determined is placed in a watch glass so that the Ptring just touches its surface.
– The knob of the torsion wire is then slowly turned till the ring is just detached from the surface.
– The reading shown by the pointer on the scale gives the force (F). The surface tension is then calculated from equation (1).
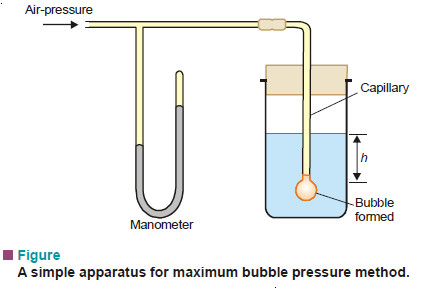
(4) Maximum Bubble Pressure Method
In this method air-pressure is applied slowly through a capillary tube dipping in the experimental liquid (See Fig)
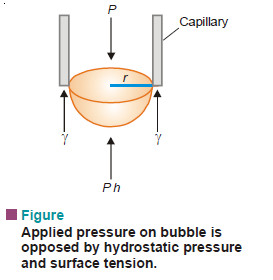
A bubble is formed at the end of the capillary. Slowly the bubble grows and becomes hemispherical. Then it breaks away when the pressure recorded by the manometer is noted. This is the maximum pressure required to make a bubble at the end of the capillary. At the moment of breaking, the forces due to maximum pressure (P) equals that of the opposing hydrostatic pressure (Ph) and the surface tension (γ) at the circumference of the capillary.
Thus,
where r = radius of capillary;
d = density of the liquid;
h = depth of liquid.
Knowing the value of P, h, d and r, γ can be found.