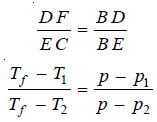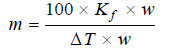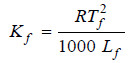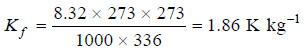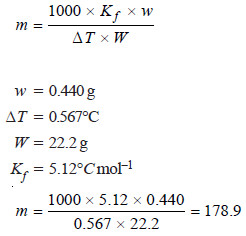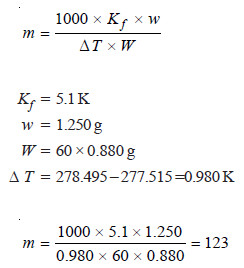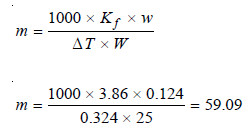Measurement of freezing point Depression
The subject of Measurement of freezing point Depression will be discused
FREEZING POINT DEPRESSION
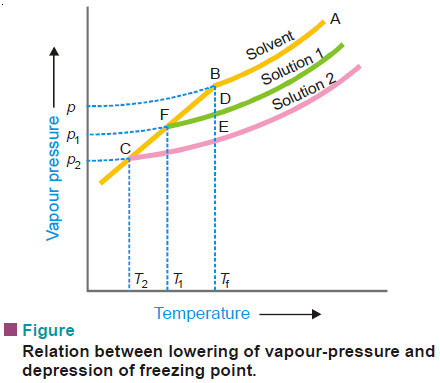
Relation between Depression of Freezing point and Lowering of Vapour-pressure
– The vapour pressure of a pure liquid changes with temperature as shown by the curve ABC, in Fig.
– There is a sharp break at B where, in fact, the freezing-point curve commences. Thus the point B corresponds to the freezing point of pure solvent, Tf.
– The vapour pressure curve of a solution (solution 1) of a nonvolatile solute in the same solvent is also shown in Fig. above.
– It is similar to the vapour pressure curve of the pure solvent and meets the freezing point curve at F, indicating that T1 is the freezing point of the solution.
– The difference of the freezing point of the pure solvent and the solution is referred to as the Depression of freezing point. It is represented by the symbol ΔT or ΔTf .
Tf – T1 = Δ T
– When more of the solute is added to the solution 1, we get a more concentrated solution (solution 2.)
– The vapour pressure of solution 2 meets the freezing-point at C, indicating a further lowering of freezing point to T2.
– For dilute solutions FD and CE are approximately parallel straight lines and BC is also a straight line. Since the triangles BDF and BEC are similar,
where p1 and p2 are vapour pressure of solution 1 and solution 2 respectively.
– Hence depression of freezing point is directly proportional to the lowering of vapour pressure.
or
ΔT ∝ p – ps …(1)
Determination of Molecular Weight from Depression of Freezing point
– Since (p) is constant for the same solvent at a fixed temperature, from (1) we can write:
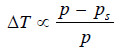
– But from Raoult’s Law for dilute solutions,
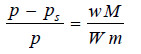
– Since M (mol wt) of solvent is constant, from (3)
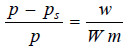
from (2) and (4)
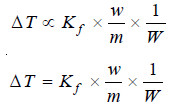
where Kf is a constant called Freezing-point constant or Cryoscopic constant or Molal depression
constant. If w/m = 1 and W = 1, Kf = ΔT. Thus,
– Molal depression constant may be defined as the freezing-point depression produced when 1 mole of solute is dissolved in one kg (1000 g) of the solvent.
If the mass of solvent (W) is given in grams, it has to be converted into kilograms. Thus the expression (5) assumes the form:
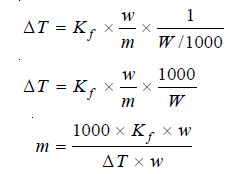
where:
m = molecular mass of solute ;
Kf = molal depression constant ;
w = mass of solute ;
ΔT = depression of F.P ;
W = mass of solvent.
– Given the value of Kf , the molecular mass of solute can be calculated.
– Sometimes the value of Kf is given in (K) per 0.1 kg. (100 g.) In that case, the expression (6) becomes:
The value of Kf . The value of Kf can be determined by measurement of ΔT by taking a solute of known molecular mass (m) and substituting the values in expression (6). The constant Kf , which is characteristic of a particular solvent, can also be calculated from the relation:
where:
Tf = freezing point of solvent in K;
Lf = molar latent heat of fusion;
R = gas constant.
Hence for water, Tf = 273 K and Lf = 336 J g–1. Therefore,
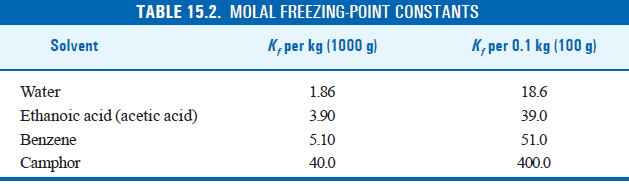
The molal depression constant for some common solvents are given in the following Table:
Solved problems on freezing-point Depression
Problem (1): 0.440 g of a substance dissolved in 22.2 g of benzene lowered the F.P of benzene by 0.567°C. Calculate the molecular mass of the substance. (Kf = 5.12°C mol–1)
Solution
We can find the molecular mass by applying the expression:
Molecular mass of substance = 178.9
Problem (2): 1.250 g of naphthalene was dissolved in 60 cm3 of benzene and F.P of the solution was found to be 277.515 K, while that of benzene 278.495 K. Density of benzene =0.880 g cm–3, Kf =5.1 K per 1000 g benzene. Calculate the molecular mass of naphthalene.
Solution
Let us apply the expression:
Thus the molecular weight of naphthalene is 123.
Problem (3): A solution of 0.124 g of a substance, X, in 25.0 l of ethanoic acid (acetic acid) has a F.P 0.324°C below that of the pure acid 16.6°C. Calculate the molecular mass (relative molecular mass) of X, given that the specific latent heat of fusion of ethanoic acid is 180.75 J g–1.
Solution
Calculation of Molal depression Constant
We know that:
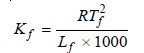
Here, freezing point of benzene, Tf = 273.2 + 16.6 = 289.8 K
Specific latent heat of fusion Lf = 180.75 J g–1
Substituting in the equation (1):
Calculation of Molecular weight
Applying the expression:
Thus the molecular weight (or relative molecular) mass of X is 59.09.
Measurement of freezing-point Depression
– The depression of freezing point can be measured more correctly and with less difficulty.
– Two simple methods commonly used are outlined below.
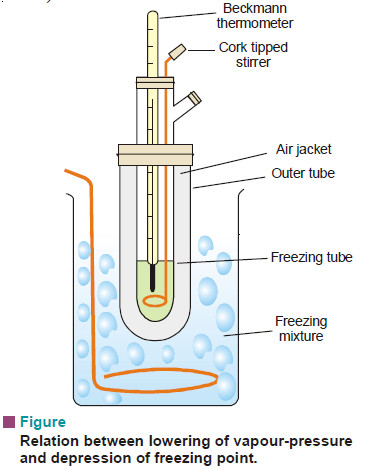
(1) Beckmann’s Method (1903)
Apparatus:
It consists of:
(i) A freezing tube with a side-arm to contain the solvent or solution, while the solute can be introduced through the side-arm;
(ii) An outer larger tube into which is fixed the freezing tube, the space in between providing an air jacket which ensures a slower and more uniform rate of cooling;
(iii) A large jar containing a freezing mixture e.g., ice and salt, and having a stirrer.
Procedure:
– 15 to 20 g of the solvent is taken in the freezing point of the solvent by directly coding the freezing point tube and the apparatus set up as shown in Fig. above so that the bulb of the thermometer is completely immersed in the solvent.
– First determine the approximate freezing point of the solvent by directly cooling the freezing point tube in the cooling bath.
– When this has been done, melt the solvent and place the freezing-point tube again in the freezing bath and allow the temperature to fall.
– When it has come down to within about a degree of the approximate freezing point determined above, dry the tube and place it cautiously in the air jacket.
– Let the temperature fall slowly and when it has come down again to about 0.5° below the freezing point, stir vigorously.
– This will cause the solid to separate and the temperature will rise owing to the latent heat set free.
– Note the highest temperature reached and repeat the process to get concordant value of freezing point.
– The F.P of the solvent having been accurately determined, the solvent is remelted by removing the tube from the bath, and a weighed amount (0.1–0.2 g) of the solute is introduced through the side tube.
– Now the freezing point of the solution is determined in the same way as that of the solvent.
– A further quantity of solute may then be added and another reading taken.
– Knowing the depression of the freezing point, the molecular weight of the solute can be determined by using the expression:
Important Precautions
– This method gives accurate results, if the following precautions are observed:
(a) The supercooling should not exceed 0.5°C.
(b) The stirring should be uniform at the rate of about one movement per second.
(c) The temperature of the cooling bath should not be 4° to 5° below the freezing point of the liquid.
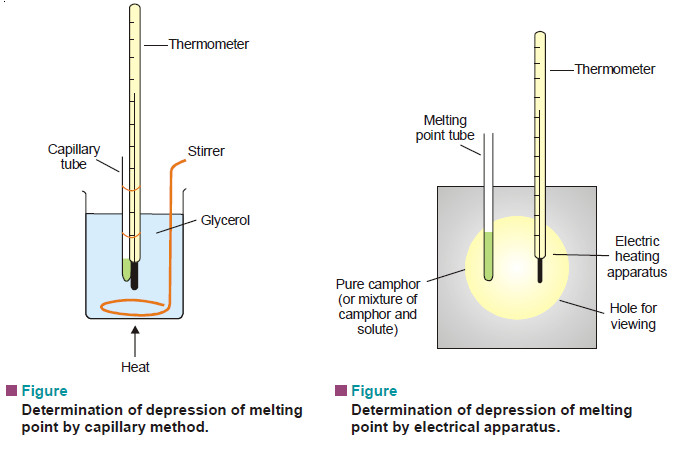
(2) Rast’s Camphor Method
– This method due to Rast (1922) is used for determination of molecular weights of solutes which are soluble in molten camphor.
– The freezing point depressions are so large that an ordinary thermometer can be used.
– Pure camphor is powdered and introduced into a capillary tube which is sealed at the upper end.
– This is tied along a thermometer and heated in a glycerol bath (see Fig. a).
– The melting point of camphor is recorded. Then a weighed amount of solute and camphor (about 10 times as much) are melted in test-tube with the open end sealed.
– The solution of solute in camphor is cooled in air.
– After solidification, the mixture is powdered and introduced into a capillary tube which is sealed. Its melting point is recorded as before.
– The difference of the melting point of pure camphor and the mixture, gives the depression of freezing point.
– In modern practice, electrical heating apparatus is used for a quick determination of melting points of camphor as also the mixture.
– The molal depression constant of pure camphor is 40°C. But since the laboratory camphor may not be very pure, it is necessary to find the depression constant for the particular sample of camphor used by a preliminary experiment with a solute of known molecular weight.
Solved problem
A sample of camphor used in the Rast method of determining molecular masses had a melting point of 176.5°C. The melting point of a solution containing 0.522 g camphor and 0.0386 g of an unknown substance was 158.8°C. Find the molecular mass of the substance. Kf of camphor per kg is 37.7.
solution
Applying the expression:
Reference: Essentials of Physical Chemistry /Arun Bahl, B.S Bahl and G.D. Tuli / multicolour edition.