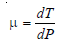Joule-Thomson Effect
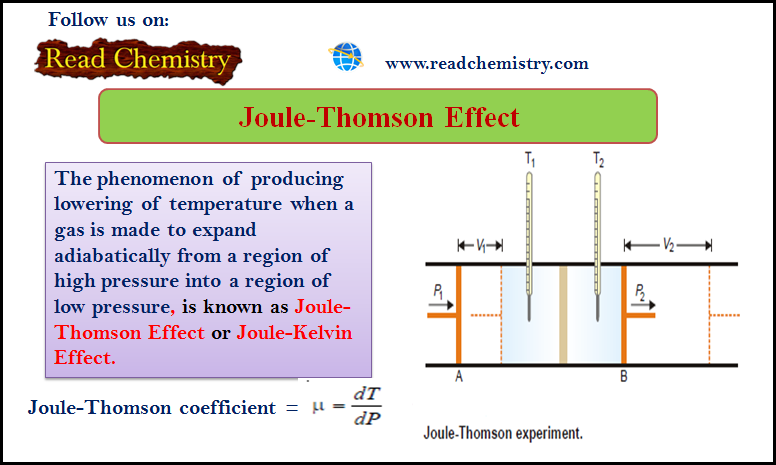
– The phenomenon of producing a lowering of temperature when a gas is made to expand adiabatically from a region of high pressure into a region of low pressure is known as the Joule-Thomson Effect or Joule-Kelvin Effect
Joule-Thomson Effect
– Joule and Thomson (later Lord Kelvin) showed that when a compressed gas is forced through a porous plug into a region of low pressure, there is appreciable cooling.
– The phenomenon of producing a lowering of temperature when a gas is made to expand adiabatically from a region of high pressure into a region of low pressure, is known as the Joule-Thomson Effect or Joule-Kelvin Effect.
Joule-Thomson Experiment
– The apparatus used by Joule and Thomson to measure the temperature change on expansion of a given volume of gas is illustrated in the following figure:
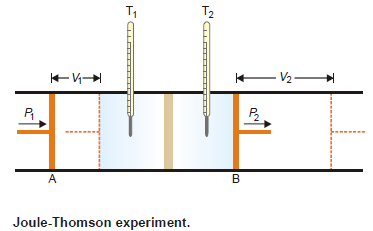
– An insulated tube is fitted with a porous plug in the middle and two frictionless pistons A and B on the sides.
– Let a volume V1 of a gas at pressure P1 be forced through the porous plug by a slow movement of piston A.
– The gas in the right-hand chamber is allowed to expand to volume V2 and pressure P2 by moving the piston B outward.
– The change in temperature is found by taking readings on the two thermometers.
– Most gases were found to undergo cooling on expansion through the porous plug.
– Hydrogen and helium were exceptions as these gases showed a warming up instead of cooling.
Explanation:
– The work done on the gas at the piston A is P1V1 and the work done by the gas at the piston B is P2V2.
– Hence the net work (w) done by the gas is:
w = P2V2 – P1V1
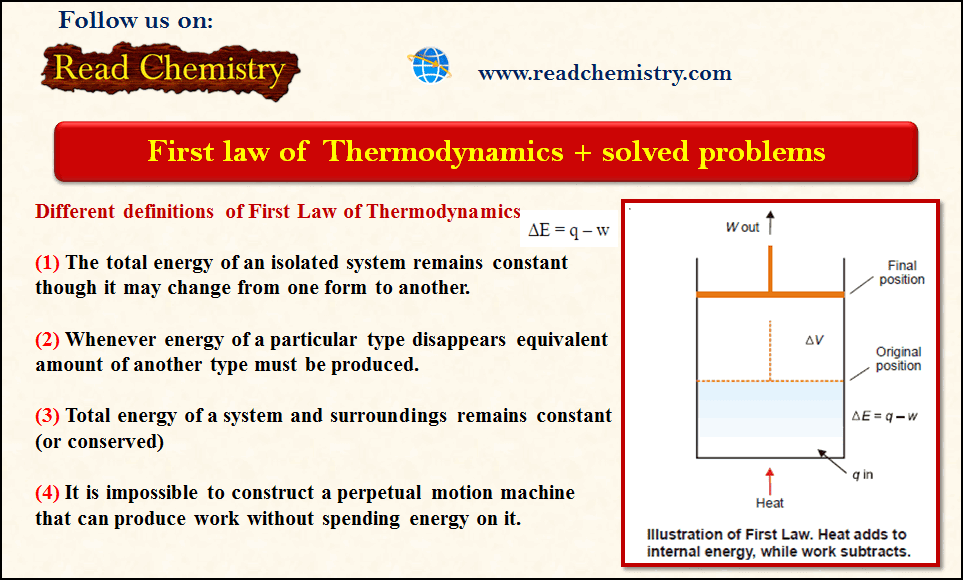
ΔE = q – w (First Law)
– But the process is adiabatic and, therefore, q = 0
ΔE = E2 – E1 = – w = – (P2V2 – P1V1)
E2 – E1 = – (P2V2 – P1V1)
– Rearranging,
E2+ P2V2 = E1 + P1V1
H2= H1 or ΔH = 0
– Thus the process in the Joule-Thomson experiment takes place at constant enthalpy.
Joule-Thomson Coefficient
– The Joule-Thomson coefficient is the number of degrees of temperature change produced per atmosphere drop in pressure under constant enthalpy conditions on passing a gas through the porous plug.
– Joule-Thomson coefficient is represented by the symbol μ.
– Thus,
– If μ is positive, the gas cools on expansion;
– If μ is negative, the gas warms on expansion.
– The temperature at which the sign changes is called the Inversion temperature.
– Most gases have positive Joule-Thomson coefficients and hence they cool on expansion at room temperature.
– Thus liquefaction of gases is accomplished by a succession of Joule-Thomson expansion.
– The inversion temperature for H2 is –80ºC. Above the inversion temperature, μ is negative.
– Thus at room temperature hydrogen warms on expansion.
– Hydrogen must first be cooled below –80ºC(with liquid nitrogen) so that it can be liquefied by further Joule-Thomson expansion. So is the case with helium.
Explanation of Joule-Thomson Effect
– We have shown above that the Joule-Thomson expansion of a gas is carried at constant enthalpy.
– But
H = E + PV
– Since H remains constant, any increase in PV during the process must be compensated by a decrease of E, the internal energy. This leads to a fall in temperature i.e., T2< T1.
– For hydrogen and helium PV decreases with the lowering of pressure, resulting in increase of E and T2> T1.
– Below the inversion temperature, PV increases with lowering of pressure, and cooling is produced.
Reference: Essentials of Physical Chemistry /Arun Bahl, B.S Bahl and G.D. Tuli / multicolor edition.