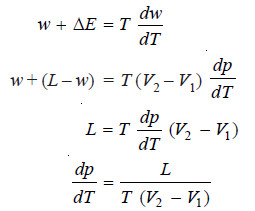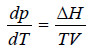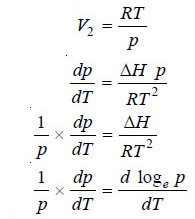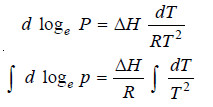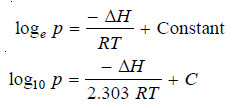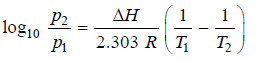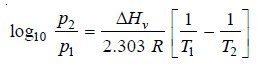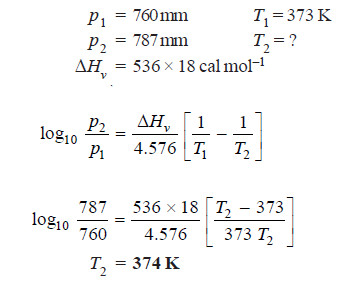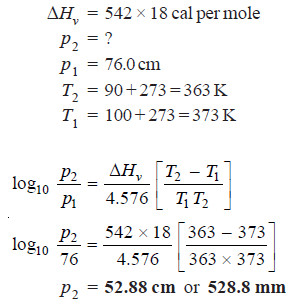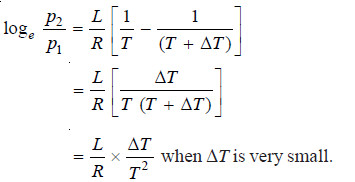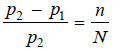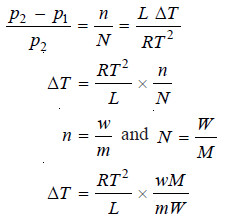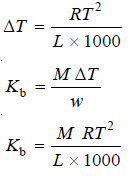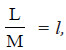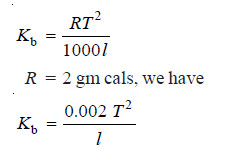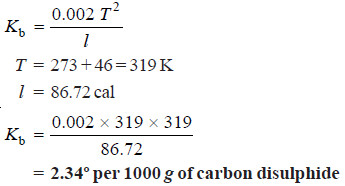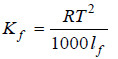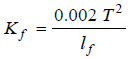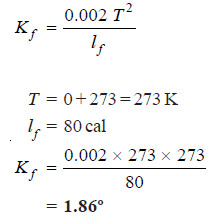Clausius-Clapeyron equation – Derivation with Applications

– In this topic, we will discuss Clausius-Clapeyron equation – Derivation with Applications.

The Clapeyron equation

– A useful thermodynamic relation which gives us important information about a system  onsisting of any two phases of a single substance in chemical equilibrium is the Clapeyron equation.

– It is derived from the Gibbs-Helmholtz equation.

– Let the system studied be

Liquid  ↔ Vapour

– Consider one gram mole of a liquid confined in a cylinder by a frictionless piston.

– Let the  volume of the liquid be V₁ and its vapour pressure equal to p.

– Now allow the liquid to evaporate reversibly at a constant temperature T and when the whole of it has vaporised, let the volume of the vapour be V₂.

∴ Work done during evaporation

w = p (V2 – V1)      ..(i)

– Differentiating equation (i) with respect to temperature at constant (V₂ – V₁), we get:

   ..(ii)

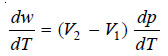
– Heat absorbed from the surroundings is the latent heat of vaporisation L which on substitution in the first law equation gives us:

ΔE = w – L   …(iii)

– On substitution of expressions (ii) and (iii) in the Gibbs-Helmholtz equation, we have

– This is the Clapeyron equation which in its general form may be written as:

…(1)

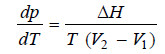
– where ΔH is the heat of transition when a volume V₁ of a definite weight of one form changes to a volume V₂ of the same weight of other form at the temperature T.

The Clausius-Clapeyron equation

– The above equation can be simplified by neglecting the small volume of the liquid in comparison with the volume of the vapour.

– Equation (1) given above in such a case becomes

– Supposing the vapour obeys the ideal gas laws:

…(2)

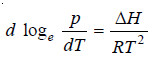
– Equation (2) above is known as the Clausius-Clapeyron equation and though approximate is of very great value.

– If ΔH is regarded as constant, we may integrate the above equation:

– If p₁ is the vapour pressure at T₁ and p₂ the vapour pressure at T₂ we have:

…(i)

…(ii)

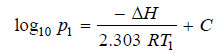
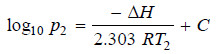
Subtracting (i) from (ii):

Applications of Clausius-Clapeyron equation

(1) Calculation of Latent Heat of Vaporisation

– If the vapour pressure of a liquid at two temperatures T₁ and T₂ be p₁ and p₂ respectively, the molar heat of vaporisation ΔH_v can be calculated by substituting these values in Clapeyron-Clausius equation.

Solved problem. If the vapour pressures of water at 95ºC and 100ºC are 634 and 760 mm respectively, calculate the latent heat of vaporisation per mole?

Solution:

– The Clapeyron Clausius equation states that:

– In a similar manner, if the vapour pressures at two different temperatures of a solid in equilibrium with its liquid phase are known, the latent heat of fusion can be calculated.

(2) Calculation of Boiling Point or Freezing Point

– If the freezing point or the boiling point of a liquid at one pressure is known, it is possible to calculate it at another pressure by the use of the Clapeyron-Clausius equation.

Solved problem. At what temperature will water boil under a pressure of 787 mm? The latent
heat of vaporisation is 536 cals per gram.

Solution:

∴ Water will boil at 101ºC under a pressure of 787 mm.

(3) Calculation of Vapour Pressure at Another Temperature

– If the mean heat of vaporisation is available, it is possible to calculate the vapour pressure of a liquid at given temperature if the vapour pressure at another temperature is known.

Solved problem. Calculate the vapour pressure of water at 90.0ºC if its value at 100.0ºC is 76.0cm. The mean heat of vaporisation of water in the temperature range 90º and 100ºC is 542 calories per gram.

Solution:

(4) Calculation of Molal Elevation Constant

– The molal elevation constant (K_b) of a solvent is defined as the elevation in boiling point which may theoretically be produced when one mole of any solute is dissolved in 1000 g of the solvent.

– Accordingly, if w g of a solute of molecular weight M is dissolved in 1000 g of the solvent and ΔT is the elevation produced, the molal elevation K_b is given by the equation:

– Let the boiling point of the pure solvent be T and that of the solvent (T + ΔT) when the atmospheric pressure is p₁.

– While p₁ is the vapour pressure of the solution at (T + ΔT) and is also the vapour pressure of the solvent at T, p₂ the vapour pressure of the solvent at (T + ΔT) can be calculated by the application of Clapeyron-Clausius equation.

– Now since (p₂ – p₁) is very small and the remainder of the terms can be neglected.

– According to Raoult’s law, the relative lowering of vapour pressure in a dilute solute is equal to the molar fraction of the solute in solution:

– When the difference between p₂ and p₁ is very small as has just been supposed, 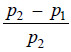be taken equal to

– If 1 mole of the solute is dissolved in 1000 g of the solvent, the above equation becomes:

l = the latent heat of vaporisation per gram of the solvent

Solved problem. The heat of vaporisation of 1 g of carbon disulphide is 86.72 calories and the boiling point is 46ºC. Calculate the molal elevation constant.

Solution:

– The molal elevation constant of a solvent is given by the expression

(5) Calculation of Molal Depression Constant

– By an exactly similar reasoning, we can calculate the molal depression constant of a solvent as:

– where lf is the latent heat of fusion per gram of the solvent,

Solved problem. The latent heat of fusion of ice per gram is 80 calories and the freezing point of water is 0ºC. Calculate the molal depression constant of water.

Solution:

– The molal depression constant of a solvent is given by the expression:

References