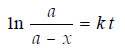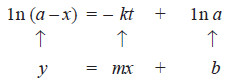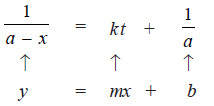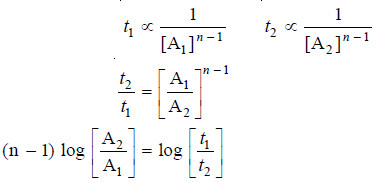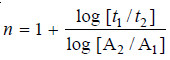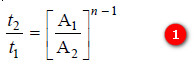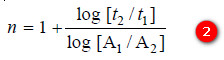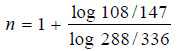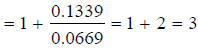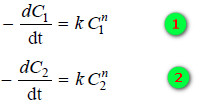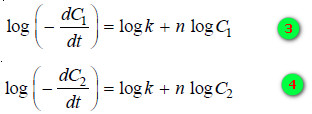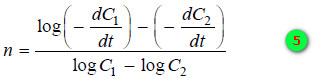How to determine the order of reaction?

Determination of the order of reaction

– There are at least four different methods to determine the order of reaction as follows:

• Using integrated rate equations
• Graphical method
• Using half-life period
• The Differential method
• Ostwald’s Isolation method

(1) Using integrated rate equations

– The reaction under study is performed by taking different initial concentrations of the reactant (a) and noting the concentration (a – x) after regular time intervals (t).

– The experimental values of a, (a – x), and t are then substituted into the integrated rate equations for the first, second, and third-order reactions.

– The rate equation which yields a constant value of k corresponds to the correct order of the reaction.

– This method of ascertaining the order of a reaction is essentially a method of hit-and-trial but was the first to be employed.

– It is still used extensively to find the order of simple reactions.

(2) Graphical method

– For reactions of type A → products, we can determine the reaction order by seeing whether a graph of the data fits one of the integrated rate equations.

In the case of First Order of reaction

– We have already derived the integrated rate equation for the first order as:

– Simplifying, it becomes:

– Thus the two variables in the first-order rate equation are:

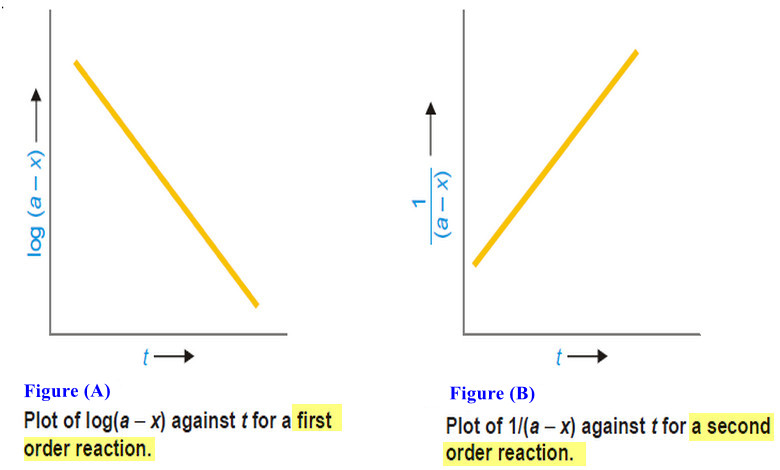
– Hence, if in is plotted against t and straight line results (see Fig A), the corresponding reaction is of the first order. However, if a curve is obtained, the reaction is not first order.

In the case of the Second Order

– We have already shown that the second-order rate equation can be written as:

– This is the equation of a straight line, y = mx + b. Here the two variables are

Thus when  is plotted against t and we get a straight line (see Fig. B), the reaction is second order.

– In case a curve is obtained, the reaction is not second order.

(3) Using half-life period

– Two separate experiments are performed by taking different initial concentrations of a reactant.

– The progress of the reaction in each case is recorded by analysis.

– When the initial concentration is reduced to one-half, the time is noted.

– Let the initial concentrations in the two experiments be [A₁] and [A₂], while times for completion of half change are t₁ and t₂ respectively.

Calculation of order of the reaction.

– We know that the half-life period for a first-order reaction is independent of the initial concentration, [A].

– We also know :

– Substituting values of initial concentrations and half-life periods from the two experiments, we
have:

– Solving for n, the order of reaction:

Solved problem: In the reduction of nitric oxide, 50% of the reaction was completed in 108 seconds when the initial pressure was 336 mm Hg and in 147 seconds initial pressure was 288 mm Hg. Find the order of the reaction.

Solution:

– We know that:

– where t₁ and t₂ are half-life periods and [A₁] and [A₂] are the corresponding initial concentrations, while n is the order of the reaction.

– Taking logs of the expression (1), we have:

– Substituting values in expression (2),

– Therefore, the reaction is of the third order.

(4) The Differential method

– This method was suggested by van’t Hoff and, therefore, it is also called van’t Hoff’s differential
method.

– According to it, the rate of a reaction of the nth order is proportional to the nth power of
concentration

– where C = concentration at any instant. In two experiments performed with different initial
concentrations, we can write:

– Taking logs of the expression (1) and (2):

– On substracting (4) from (3), we get:

– To find n, 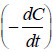in the two experiments is determined by plotting concentrations against time (t).

– The slope, 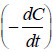at a given time interval is measured by drawing tangents.

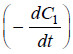
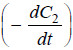
– Using the values of slopes and   in the equation (5), n can be calculated.

 

(5) Ostwald’s Isolation method

– This method is employed in determining the order of complicated reactions by (isolating) one of
the reactants so far as its influence on the rate of reaction is concerned.

– Suppose the reaction under consideration is :

A + B + C → products

– The order of the reaction with respect to A, B and C is determined.

– For the determination of the order of the reaction with respect to A, B and C are taken in a large excess so that their concentrations are not affected during the reaction.

– The order of the reaction is then determined by using any of the methods described earlier. Likewise, the order of the reaction with respect to B and C is determined.

– If n_A, n_B and n_C are the orders of the reaction with respect to A, B and C respectively, the order of the reaction n is given by the expression.

n = n_A + n_B + n_C