Laws of Osmotic Pressure
Laws of Osmotic Pressure
– From a study of the experimental results obtained by Pfeffer, van’t Hoff showed that for dilute solutions :
(a) The osmotic pressure of a solution at a given temperature is directly proportional to its concentration.
(b) The osmotic pressure of a solution of a given concentration is directly proportional to the absolute temperature.
– From the above findings, van’t Hoff (1877) established the laws of osmotic pressure and pointed out that these were closely related to the gas laws.
(1) Boyle-van’t Hoff Law for Solutions
– If π is the osmotic pressure and C its concentration, from (a) we can write π ∝ C, if temperature is constant.
– If the concentration of the solute is expressed in moles per litre and V is the volume of the solution that contains 1 mol of solute,
– This relationship is similar to the Boyle’s law for gases and is known as the Boyle-van’ t Hoff law for solutions.
(2) Charles-van’t Hoff Law for Solutions
– If T is the absolute temperature, from the statement (b), we can write:
π ∝ T, if temperature is constant
– This relationship is similar to the Charles’ Law for gases and is known as Charles-van’t Hoff law for solutions.
(3) Van’t Hoff Equation for Solutions
– As shown above the osmotic pressure (π) of a dilute solution is inversely proportional to the volume (V) containing 1 mole of the solute and is directly proportional to the absolute temperature (T).
This is,
Combining (1) and (2) van’t Hoff gave the general relationship
π V = R’ T …(3)
where R’ is a constant.
– He showed that this equation was parallel to the general Gas Equation (PV = RT), as the value of R’ calculated from the experimental values of π, V, and T came out to be almost the same as of the Gas constant, R.
– It is noteworthy that the van’t Hoff Equation (3) was derived for 1 mole of solute dissolved in V litres.
– If n moles of solute are dissolved in V litres of solution, this equation assumes the form
π V = n R T
Solved problem 1. A solution of cane-sugar (mol mass = 342) containing 34.2 g litre–1 has an osmotic pressure of 2.4 atm at 20°C. Calculate the value of R in litre-atmospheres.
Solution
From van’t Hoff equation
where:
π = osmotic pressure,
V = volume of solution in litres containing 1 mole of solute,
T = absolute temperature.
In the present case,
Substituting the values in the expression (1),
Solved problem 2. Experiment shows that 10 g of cane sugar (mol mass = 342) in 1 × 10–3 m3 of solution produces an osmotic pressure of 6.68 × 104 N m–2 at 273 K. Calculate the value of R in SI units.
Solution
Substituting the values in van’t Hofff equation,
(4) Avogadro-van’t Hoff Law for Solutions
– Writing Van’t Hoff equation for two different dilute solutions,
π1V1 = n1 RT1 …(1)
π2V2 = n2 RT2 ..(2)
where n1 and n2 are the number of moles (molecules) of the solute in V1 and V2 litres of the two solutions.
– If π1 = π2 and T1 = T2, it follows from (1) and (2) that:
– Hence when osmotic pressure and temperature are the same, equal volumes of solutions would contain equal number of moles (molecules) of the solute.
– This relationship is analogous to Avogadro’s law of gases and is referred to as Avogadro-van’t Hoff law for solutions. Alternatively, this law may be stated as:
Isotonic solutions at the same temperature have equimolar concentrations.
Van’t Hoff theory of dilute solution
– Van’t Hoff noted the striking resemblance between the behaviour of dilute solutions and gases.
– Dilute solutions obeyed laws analogous to the gas laws.
– To explain it van’t Hoff visualised that gases consist of molecules moving in vacant space (or vacuum), while in solutions the solute particles are moving in the solvent.
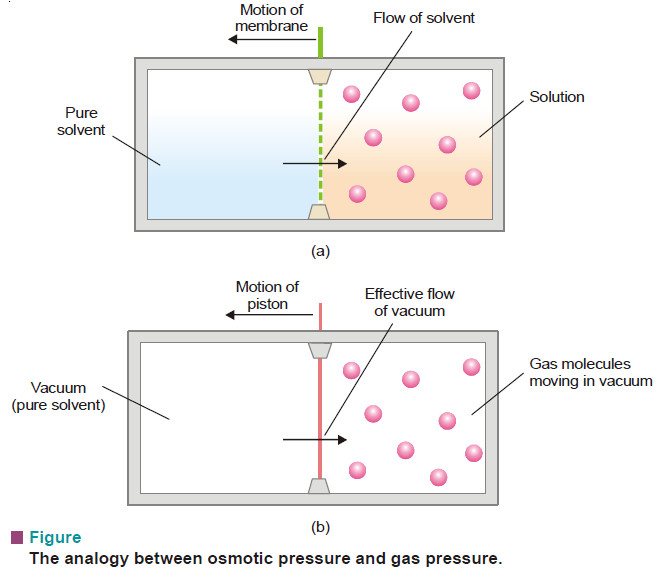
– The exact parallelism between solutions and gases is illustrated by experimental demonstration shown in the following Fig.
– As shown in Fig.(a), the pure solvent flows into the solution by osmosis across the semipermeable membrane.
– The solute molecules striking the membrane cause osmotic pressure and the sliding membrane is moved towards the solvent chamber.
– In case of a gas (Fig.b), the gas molecules strike the piston and produce pressure that pushes it towards the empty chamber.
– Here it is the vacuum which moves into the gas. This demonstrates clearly that there is close similarity between a gas and a dilute solution.
– Thinking on these lines, van’t Hoff propounded his theory of dilute solution.
Statement of van’t Hoff theory
– The van’t Hoff theory of dilute solutions states that :
(a substance in solution behaves exactly like a gas and the osmotic pressure of a dilute solution is equal to the pressure which the solute would exert if it were a gas at the same temperature occupying the same volume as the solution).
– Suppose a dilute sugar solution to be contained in an exactly full, covered beaker. Then suppose the water to vanish, leaving the sugar molecules suspended in otherwise empty space. The sugar would then function as a gas, exerting pressure equal to its former osmotic pressure.
– According to the van’t Hoff theory of dilute solutions, all laws or relationship obeyed by gases would be applicable to dilute solutions.
– From van’t Hoff theory it follows that just as 1 mole of a gas occupying 22.4 litres at 0°C exerts 1 atmosphere pressure, so, 1 mole of any solute dissolved in 22.4 litres would exert 1 atmosphere osmotic pressure.
– van’t Hoff theory holds only for dilute solutions and if there is no dissociation or association of the solute molecules.
Calculations of osmotic pressure
As shown above, all gas laws may be considered to apply to dilute solutions rigidly. This gives an easy solution to problems on osmotic pressure.
Solved problem 1. Calculate the osmotic pressure of a 5% solution of glucose (mol wt = 180) at 18°C.
Solution
From van’t Hoff Equation:
πV = nRT
where:
π = osmotic pressure in atmospheres;
V = volume in litres; n = number of moles of solute,
(w/M), w being the weight in grams and M its molecular weight;
R = gas constant.
In this case :
Solved problem 2. Find the osmotic pressure in millimetres of mercury at 15°C of a solution of naphthalene (C10H8) in benzene containing 14 g of naphthalene per litre of solution.
Solution
from vant Hoff equation
Solved problem 3. Calculate the osmotic pressure of solution obtained by mixing
(a) 100 ml of 3.4 per cent solution of urea (mol mass = 60) and
(b) 100 ml of 1.6 per cent solution of cane sugar (mol mass = 342) at 20°C.
Solution
Osmotic pressure of urea
πV = nRT
According to the van’t Hoff theory of dilute solutions, dissolved substances behave like gases. Thus they obey Dalton’s Law of Partial Pressures. Hence the total osmotic pressure of the mixture
= 6.81 + 0.56 = 7.37 atm
Determination of Molecular weight from Osmotic Pressure
– Osmotic pressure measurements are less accurate and difficult to carry out. Therefore, this method is not widely used in the determination of molecular weights.
– The chief use of this method is in finding molecular weights of polymers e.g., plastics, proteins, and starch, which have very high molecular weights.
– Knowing the osmotic pressure of a given solution, the molecular weight of the solute can be calculated as follows from van’t Hoff equation
Solved problem 1.Morse and Frazer observed that a solution of glucose containing 18 grams per litre had an osmotic pressure of 2.39 atmospheres at 23°C. Find the molecular weight of glucose.
Solution
Solved problem 2. A solution of glycol containing 1.821 g per litre has an osmotic pressure of 51.8 cm of mercury at 10°C. What is the molecular mass of glycol?
Solution
We know that from van’t Hoff equation
Relation between Vapour pressure and Osmotic pressure
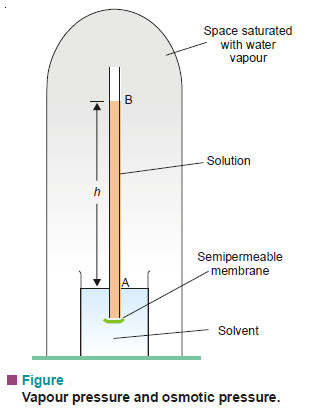
– Consider an aqueous solution contained in a tube closed at the lower end by a semipermeable membrane and immersed in pure water (Fig).
– The whole apparatus is enclosed under a bell-jar which is evacuated. When the osmotic equilibrium is reached, the bell jar is saturated with water vapour.
– Let the height of solution in the tube be h cm. If the solution is sufficiently dilute, the density of the solution will be approximately the same as that of the pure solvent, d.
– Since at equilibrium, the osmotic pressure of solution (π) is exactly balanced by hydrostatic pressure due to h cm column of solution of density d, we can write,
π = h × d ….(1)
If p is the vapour pressure of the solvent at the given temperature and p, the vapour pressure of the solution, the pressure at all points on a level with A will be p and at all points on a level with B will be ps. Now, the pressure at A is greater than at B due to the weight of the column of solvent vapour of height h. Thus,
p – ps = hD …(2)
where D = density of solvent vapour at pressure p.
Dividing (1) by (2), we have:
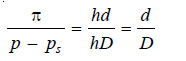
At a given temperature, d and D are constant. That is
This shows that osmotic pressure is directly proportional to the lowering of vapour pressure.
Relative Lowering of Vapour Pressure and Osmotic Pressure
When the osmotic equilibrium is established in apparatus shown in Fig. 16.21, we have
π = h × d, for dilute solution …(1)
p – ps = h × D, for solvent vapour …(2)
Dividing (2) by (1) and simplifying
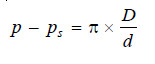
where D is the density of the solvent vapour and d is the density of the solution.
From the gas equation for one mole of the solvent vapour (pV = RT)
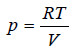
If M is the molecular mass of the solvent vapour, its density
Substituting the value of V in equation (4)
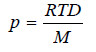
Dividing (3) by (5)
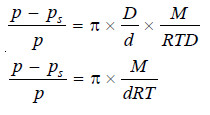
At a fixed temperature d is constant and hence the factorM/dRT has a constant value. Therefore we can write
That is, relative lowering of vapour pressure is directly proportional to osmotic pressure.
Derivation of Raoult’s law
According to van’t Hoff equation for solutions,
πV = nRT
where V = volume of solution and n = number of moles of solute.
where N = number of moles of the solvent.
This is the Raoult’s law equation in which n is the denominator is ignored when the solution is very dilute.


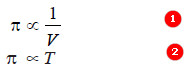
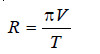
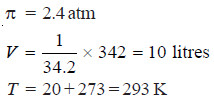
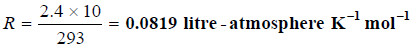
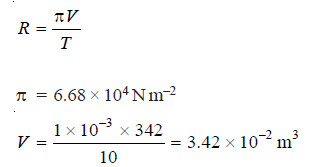
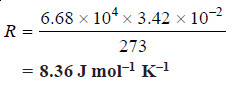
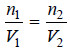
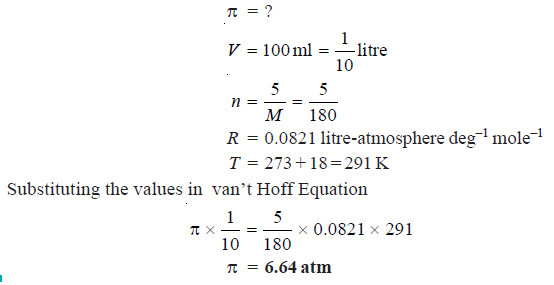
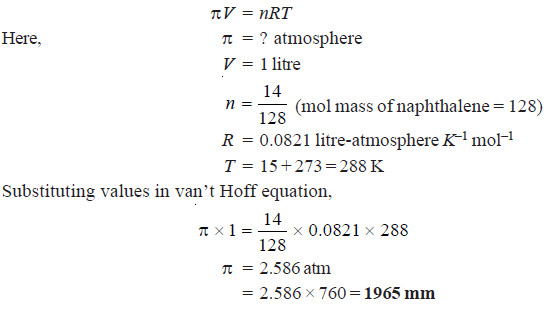

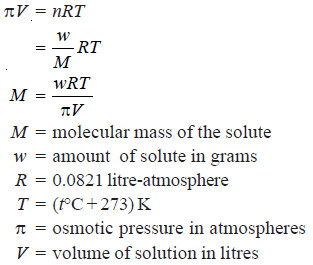
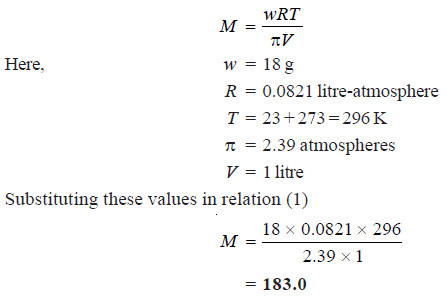

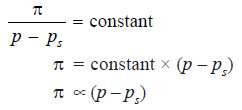
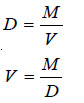
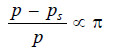

Great and excellent time spent. Thanks.