Organic Chemistry
The Relative Stabilities of Cycloalkanes: Ring Strain
The Relative Stabilities of Cycloalkanes: Ring Strain
** Cycloalkanes do not all have the same relative stability. Experiments have shown that cyclohexane is the most stable cycloalkane and that, in comparison, cyclopropane and cyclobutane are much less stable. This difference in relative stability is due to ring strain, which comprises angle strain and torsional strain.
** Angle strain is the result of deviation from ideal bond angles caused by inherent structural constraints (such as ring size).
** Torsional strain is the result of repulsive dispersion forces that cannot be relieved due to restricted conformational mobility.
(1) Ring Strain in Cyclopropane
** The carbon atoms of alkanes are sp3 hybridized.
** The normal tetrahedral bond angle of an sp3 -hybridized atom is 109.5o.
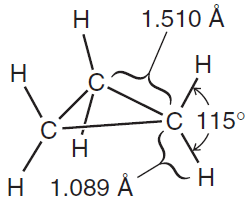
** In cyclopropane (a molecule with the shape of a regular triangle), the internal angles must be 608 and therefore they must depart from this ideal value by a very large amount—by 49.5o:
** Angle strain exists in a cyclopropane ring because the sp3 orbitals comprising the carbon–carbon σ bonds cannot overlap as effectively (Fig. 1) as they do in alkanes (where perfect end-on overlap is possible).
** The carbon–carbon bonds of cyclopropane are often described as being “bent.” Orbital overlap is less effective. (The orbitals used for these bonds are not purely sp3; they contain more p character.)
** The carbon–carbon bonds of cyclopropane are weaker, and as a result the molecule has greater potential energy.
Fig(1): Orbital overlap in the carbon–carbon bonds of cyclopropane cannot occur perfectly end-on. This leads to weaker “bent” bonds and to angle strain
** While angle strain accounts for most of the ring strain in cyclopropane, it does not account for it all. Because the ring is (of necessity) planar, the C-H bonds of the ring are all eclipsed (Fig. 2 , 3), and the molecule has torsional strain from repulsive dispersion forces as well.
Fig(2): Bond distances and angles in cyclopropane
Fig(3): A Newman projection formula as viewed along one carbon– carbon bond shows the eclipsed hydrogens. (Viewing along either of the other two bonds would show the same picture.)
(2) Ring Strain in Cyclobutane
** Cyclobutane also has considerable angle strain.
** The internal angles are 88o—a departure of more than 21o from the normal tetrahedral bond angle.
** The cyclobutane ring is not planar but is slightly “folded” (Fig. 4).
** If the cyclobutane ring were planar, the angle strain would be somewhat less (the internal angles would be 90o instead of 88o), but torsional strain would be considerably larger because all eight C-H bonds would be eclipsed.
** By folding or bending slightly the cyclobutane ring relieves more of its torsional strain than it gains in the slight increase in its angle strain.
Figure (4) The “folded” or “bent” conformation of cyclobutane.
(3) Ring Strain in Cyclopentane
** The internal angles of a regular pentagon are 108o, a value very close to the normal tetrahedral bond angles of 109.5o.Therefore, if cyclopentane molecules were planar, they would have very little angle strain.
** Planarity, however, would introduce considerable torsional strain because all ten C-H bonds would be eclipsed.
** Consequently, like cyclobutane, cyclopentane assumes a slightly bent conformation in which one or two of the atoms of the ring are out of the plane of the others (Fig. 5). This relieves some of the torsional strain.
** Slight twisting of carbon–carbon bonds can occur with little change in energy and causes the out-of-plane atoms to move into plane and causes others to move out. Therefore, the molecule is flexible and shifts rapidly from one conformation to another.
** With little torsional strain and angle strain, cyclopentane is almost as stable as cyclohexane.
Figure(5) The “bent” or “envelope” form of cyclopentane. In this structure the front carbon atom is bent upward. In actuality, the molecule is flexible and shifts conformations constantly.
Reference: Organic chemistry / T.W. Graham Solomons , Craig B.Fryhle , Scott A.snyder , / ( eleventh edition) / 2014.