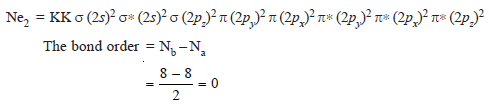Read Chemistry
Molecular Orbitals for Homonuclear Diatomic Molecules
– In the previous subject, we talk about but electronic structures and bonding properties of some of The Heteronuclear Diatomic Molecules. but in this subject, we will talk about Molecular Orbitals for Homonuclear Diatomic Molecules (MO Theory)
– After having discussed the basic principles of Molecular Orbital Theory, we are now able to take up the electronic structures and bonding properties of some of the homonuclear diatomic molecules.
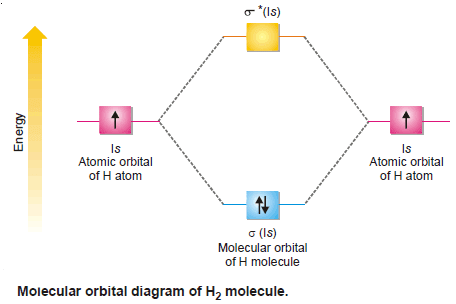
(1) Molecular Orbitals for Hydrogen, H2
– The hydrogen molecule is formed from 1s1 atomic orbitals of two atoms.
– They give rise to two molecular orbitals σ(1s) and σ*(1s).
– The molecule has two electrons to be accommodated in these two molecular orbitals and are filled as desired by Aufbau’s order of filling.
– Both these electrons go to the lower energy bonding molecular orbital and the antibonding orbital remains vacant.
– The electronic configuration of the molecule is represented by the equation:
– The number of bonds in the molecule, accordingly is = ½ (2 – 0) = 1.
– Thus two hydrogen atoms are bonded through only one bond in the molecule.
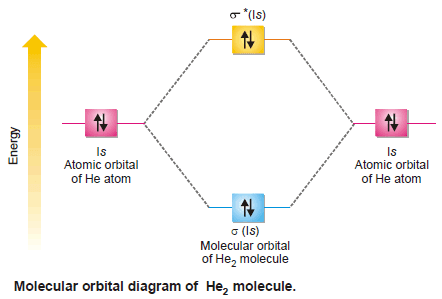
(2) Molecular Orbitals for Helium, He2
– Helium atoms have the configuration 1s2.
– For the formation of He2, the molecular orbitals required are σ (1s) and σ* (1s) which have to accommodate four electrons (two each contributed by the atoms).
– Each one of these molecular orbitals would accommodate two electrons as shown below.
– The molecule of helium is represented by the equation:
– There are two electrons in each of the bonding and antibonding orbitals giving zero as the number of bonds, ½(2 – 2) = 0 i.e., this molecule does not exist.
(3) Molecular Orbitals for Lithium, Li2
– Lithium atom has one electron in the valence shell 2s1, the other electrons are non-bonding.
– Two such atoms give a molecule having two molecular orbitals σ (2s) and σ* (2s) and only two electrons are to be filled in them.
– These are accommodated in the molecular bonding orbital while the antibonding molecular orbital remains vacant.
– The number of bonds = ½[(2 – 0)] = 1 i.e., two lithium atoms form a molecule involving a single covalent bond.
– The bond energy is about 25 kcal mole–1 which is much less than of H2 molecule (103 kcal mole-1).
(4) Molecular Orbitals for Beryllium, Be2
– A diatomic beryllium molecule is not formed because two valence electrons present as 2s2 in Be atoms give two molecular orbitals σ (2s) and σ* (2s), each having two electrons.
– The equation representing the formation is:
– The number of bonds = ½(2 – 2) = 0.
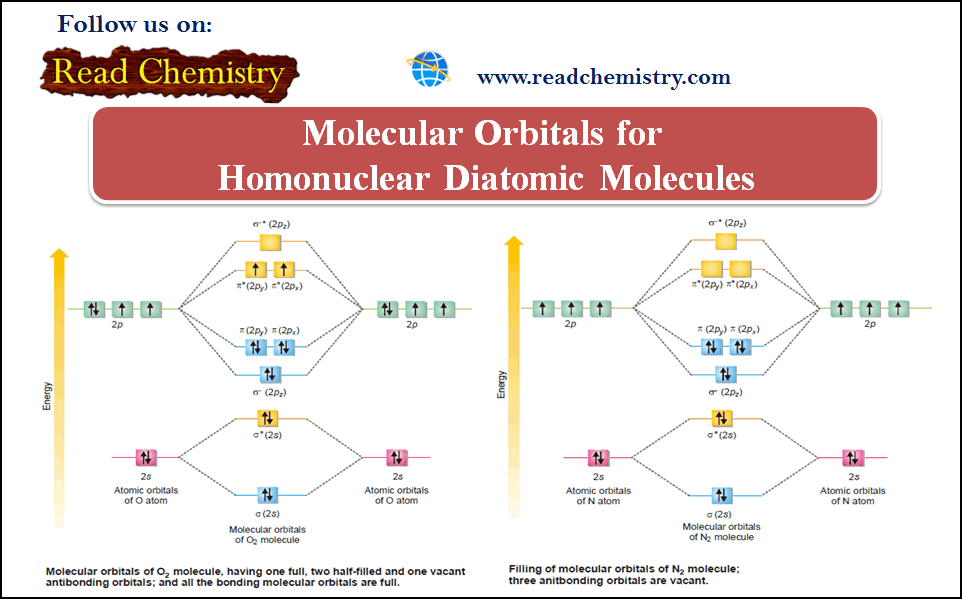
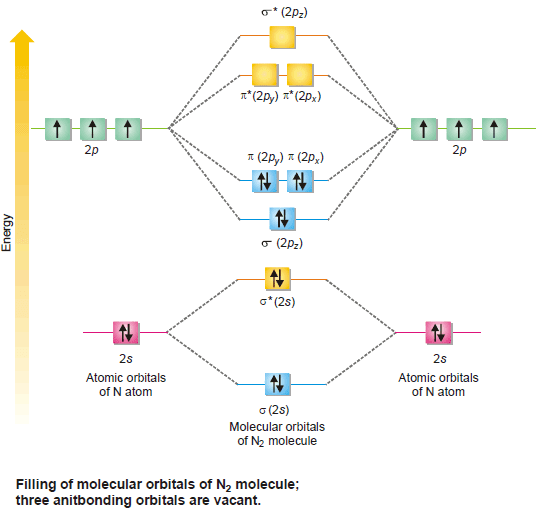
(5) Nitrogen, N2
– Each of the two N-atoms 1s2 , 2s2 , 2px1, 2py1 , 2pz1 contribute, (2 + 1 + 1 + 1) = 5 valence electrons and four atomic orbitals towards the molecule.
– The molecule would have eight molecular orbitals and ten electrons to be accommodated in them.
– The electronic configuration in the molecule is represented as given in the following figure:
– There are eight electrons in the bonding molecular orbitals and only two in the antibonding orbital.
– This gives the number of bonds ½(8 – 2) = 3.
– The two N atoms are bonded with three covalent bonds i.e., a triple bond.
– N2 molecule is diamagnetic as it has no unpaired electron.
(6) Oxygen, O2
– The two participating oxygen atoms 1s2 , 2s2 , 2px2, 2py1 , 2pz1 contribute a total of 2(2 + 2 + 1+ 1) = 12 valence electrons and 2 × 4 = 8 atomic orbitals towards the oxygen molecule.
– There are eight molecular orbitals and 12 electrons are accommodated as shown in the following figure:
– We find from the figure above that the Aufbau order of filling of molecular orbital leaves two unpaired electrons in each of degenerate πy* (2py) and πz* (2px) orbitals.
– The electronic configuration of the molecular orbitals accounts admirably for the paramagnetic behavior of oxygen molecule.
– It is the lone electron that creates a magnetic field around it due to its spin.
– But if there are two electrons spinning near each other in opposite directions i.e., with their spins paired, the magnetic fields created by these electrons cancel each other. However, if the electrons spin in the same direction, the total magnetic field would be the sum of the fields of each of the two electrons.
– This situation prevails in oxygen molecule and the experimentally established extent or magnitude of paramagnetism is consistent with two unpaired electrons per molecule.
– This is the greatest success of the Molecular Orbital theory.
– The number of bonds in O2 molecules = ½(8 – 4) = 2.
– Proceeding on these lines, the electronic configurations of other simple species like O2– , O2+ can be worked out.
– The electronic configuration, bond order and magnetic character of these species is summed in the following table:
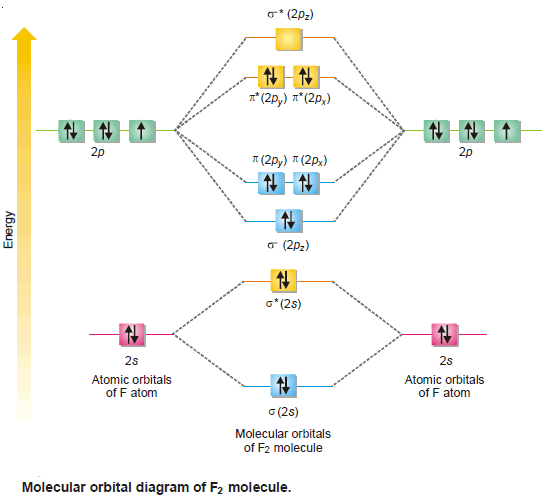
(7) Fluorine, F2
– The two participating F atoms 1s2 , 2s2 , 2px2, 2py2 , 2pz1 contribute a total of 14 valence electrons and there are eight molecular orbitals towards F2 molecule formed from two F atoms having four atomic orbitals each.
– In these MOs, 14 electrons are accommodated.
– The electronic configuration of F2 molecule is:
– Since F2 molecule has no unpaired electron, it is diamagnetic in nature.
– The molecular orbital diagram of F2 molecule is shown in the following figure:
(8) Neon Molecule, Ne2
– The electronic configuration of Ne is 1s2 2s2 2p6. There are 16 valence electrons belonging to both neon atoms.
– There are 8 MOs which have to accommodate 16 valence electrons.
– The electronic configuration of Ne2 molecule is given below:
– Since no bond is formed between two Ne atoms, this molecule does not exist.
Reference: Essentials of Physical Chemistry /Arun Bahl, B.S Bahl and G.D. Tuli / multicolor edition.
