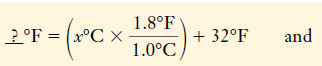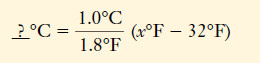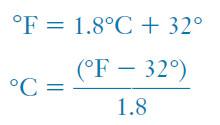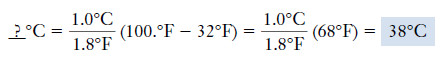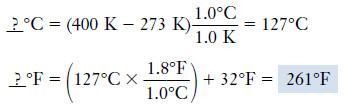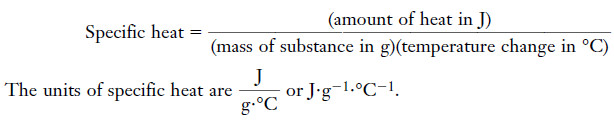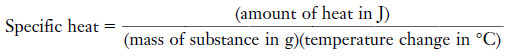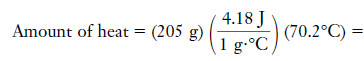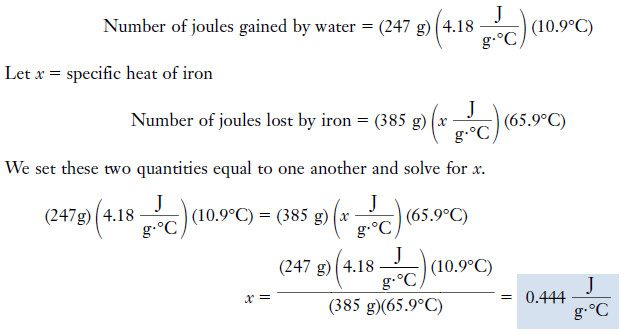Heat and Temperature
Difference Between Heat and Temperature
– Heat is one form of energy.
– Many forms of energy can be interconverted and that in chemical processes, chemical energy is converted to heat energy or vice versa.
– The amount of heat a process uses (endothermic) or gives off (exothermic) can tell us a great deal about that process.
– For this reason it is important for us to be able to measure the intensity of heat.
– Temperature measures the intensity of heat, the “hotness” or “coldness” of a body.
– A piece of metal at 100°C feels hot to the touch, whereas an ice cube at 0°C feels cold. Why?
– Because the temperature of the metal is higher, and that of the ice cube lower, than body temperature.
– Heat is a form of energy that always flows spontaneously from a hotter body to a colder body—never in the reverse direction.
– Temperatures can be measured with mercury-in-glass thermometers.
– A mercury thermometer consists of a reservoir of mercury at the base of a glass tube, open to a very thin (capillary) column extending upward.
– Mercury expands more than most other liquids as its temperature rises.
– As it expands, its movement up into the evacuated column can be seen.
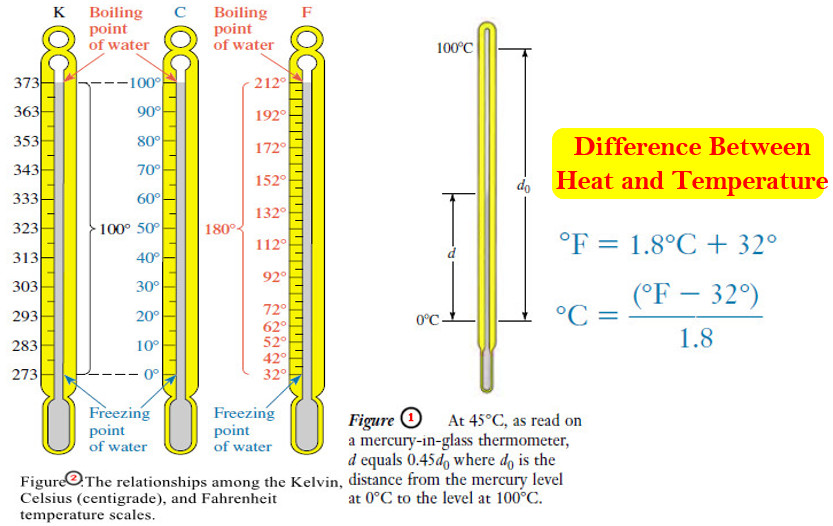
Celsius temperature scale
– Anders Celsius (1701–1744), a Swedish astronomer, developed the Celsius temperature scale, formerly called the centigrade temperature scale.
– When we place a Celsius thermometer in a beaker of crushed ice and water, the mercury level stands at exactly 0°C, the lower reference point.
– In a beaker of water boiling at one atmosphere pressure, the mercury level stands at exactly 100°C, the higher reference point.
– There are 100 equal steps between these two mercury levels.
– They correspond to an interval of 100 degrees between the melting point of ice and the boiling point of water at one atmosphere.
– Figure (1) shows how temperature marks between the reference points are established.
Fahrenheit temperature scale
– In the United States, temperatures are frequently measured on the temperature scale devised by Gabriel Fahrenheit (1686–1736), a German instrument maker.
– On this scale the freezing and boiling points of water are defined as 32°F and 212°F, respectively.
Kelvin temperature scale
– In scientific work, temperatures are often expressed on the Kelvin (absolute) temperature scale.
– the zero point of the Kelvin temperature scale is derived from the observed behavior of all matter.
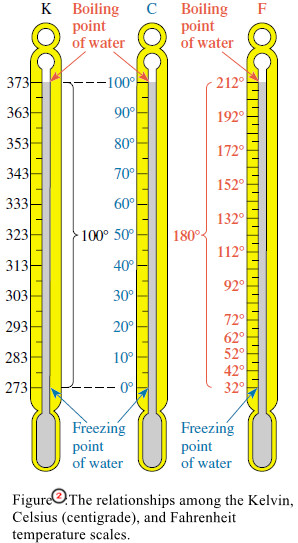
Relationships among Celsius, Fahrenheit, Kelvin temperature scales
– Relationships among the three temperature scales are illustrated in Figure (2).
– Between the freezing point of water and the boiling point of water, there are 100 steps (°C or kelvins, respectively) on the Celsius and Kelvin scales.
– Thus the “degree” is the same size on the Celsius and Kelvin scales.
– But every Kelvin temperature is 273.15 units above the corresponding Celsius temperature.
– The relationship between these two scales is as follows:
– In the SI system, “degrees Kelvin” are abbreviated simply as K rather than °K and are called kelvins.
– Any temperature change has the same numerical value whether expressed on the Celsius scale or on the Kelvin scale.
– For example, a change from 25°C to 59°C represents a change of 34 Celsius degrees.
– Converting these to the Kelvin scale, the same change is expressed as (273 + 25) = 298 K to (59 + 273) = 332 K, or a change of 34 kelvins.
– Comparing the Fahrenheit and Celsius scales, we find that the intervals between the same reference points are 180 Fahrenheit degrees and 100 Celsius degrees, respectively.
– Thus a Fahrenheit degree must be smaller than a Celsius degree. It takes 180 Fahrenheit degrees to cover the same temperature interval as 100 Celsius degrees.
– From this information, we can construct the unit factors for temperature changes:
– These are often remembered in abbreviated form:
– But the starting points of the two scales are different, so we cannot convert a temperature on one scale to a temperature on the other just by multiplying by the unit factor.
– In converting from °F to °C, we must subtract 32 Fahrenheit degrees to reach the zero point on the Celsius scale (Figure 2).
Solved problems on Heat and Temperature
Example (1): When the temperature reaches “100.°F in the shade,” it’s hot. What is this temperature on the Celsius scale?
Plan
– We use the relationship:
to carry out the desired conversion.
Solution:
Example (2): When the absolute temperature is 400 K, what is the Fahrenheit temperature?
Plan
We first use the relationship:
__ ? °C= K + 273°
to convert from kelvins to degrees Celsius, then we carry out the further conversion from degrees Celsius to degrees Fahrenheit.
Solution:
Heat Transfer and The Measurements of Heat
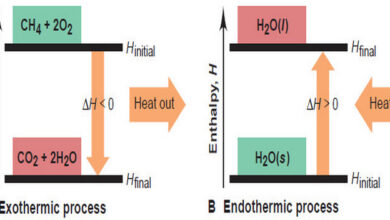
– Chemical reactions and physical changes occur with either the simultaneous evolution of heat (exothermic processes) or the absorption of heat (endothermic processes).
– The amount of heat transferred in a process is usually expressed in joules or in calories.
– The SI unit of energy and work is the joule (J), which is defined as 1 kg.m2/s2.
– The kinetic energy (KE) of a body of mass m moving at speed v is given by 1/2 mv2.
– A 2-kg object moving at one meter per second has KE = 1/2(2 kg)(1 m/s)2 =1 kg.m2/s2 = 1 J.
– You may find it more convenient to think in terms of the amount of heat required to raise the temperature of one gram of water from 14.5°C to 15.5°C, which is 4.184 J.
– One calorie is defined as exactly 4.184 J.
– The so-called “large calorie,” used to indicate the energy content of foods, is really one kilocalorie, that is, 1000 calories. We shall do most calculations in joules.
The specific heat
– The specific heat of a substance is the amount of heat required to raise the temperature of one gram of the substance one degree Celsius (also one kelvin) with no change in phase.
– Changes in phase (physical state) absorb or liberate relatively large amounts of energy .
– The specific heat of each substance, a physical property, is different for the solid, liquid, and gaseous phases of the substance.
– For example, the specific heat of ice is 2.09 J/g.°C near 0°C; for liquid water it is 4.18 J/g.°C; and for steam it is 2.03 J/g.°C near 100°C.
– The specific heat for water is quite high.
The heat capacity
– The heat capacity of a body is the amount of heat required to raise its temperature 1°C.
– So, The heat capacity of a body is its mass in grams times its specific heat.
– The heat capacity refers to the mass of that particular body, so its units do not include mass. The units are J/°C or J.°C-1.
Solved problems on The specific heat
Example (1): How much heat, in joules, is required to raise the temperature of 205 g of water from 21.2°C to 91.4°C?
Plan
– The specific heat of a substance is the amount of heat required to raise the temperature of 1 g of substance 1°C:
– We can rearrange the equation so that:
(Amount of heat) = (mass of substance) (specific heat) (temperature change)
– Alternatively, we can use the unit factor approach.
Solution:
By the unit factor approach,
– All units except joules cancel. To cool 205 g of water from 91.4°C to 21.2°C, it would be necessary to remove exactly the same amount of heat, 60.2 kJ
– When two objects at different temperatures are brought into contact, heat flows from the hotter to the colder body (Figure 3); this continues until the two are at the same temperature.
– We say that the two objects are then in thermal equilibrium.
– The temperature change that occurs for each object depends on the initial temperatures and the relative masses and specific heats of the two materials.
Example (2): A 385-gram chunk of iron is heated to 97.5°C. Then it is immersed in 247 grams of water originally at 20.7°C. When thermal equilibrium has been reached, the water and iron are both at 31.6°C. Calculate the specific heat of iron.
Plan
– The amount of heat gained by the water as it is warmed from 20.7°C to 31.6°C is the same as the amount of heat lost by the iron as it cools from 97.5°C to 31.6°C.
– We can equate these two amounts of heat and solve for the unknown specific heat.
Solution
Temperature change of water = 31.6°C – 20.7°C = 10.9°C
Temperature change of iron = 97.5°C – 31.6°C = 65.9°C
References
- Principles of Inorganic Chemistry / Brian W. Pfennig / 1st ed, 2015 /John Wiley & Sons, Inc/ USA.
- Inorganic Chemistry /Peter Atkins, Tina Overton, Jonathan Rourkel, Mark Weller, Fraser Armstrong, Mike Hagerman / 6th ed, 2014 /W. H. Freeman and Company/ New York, USA.
-