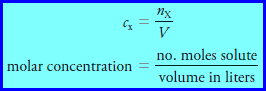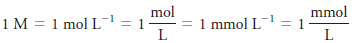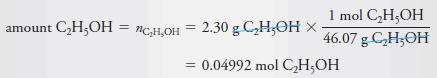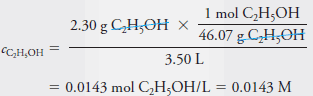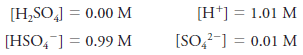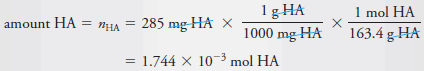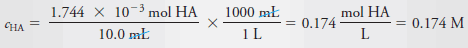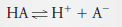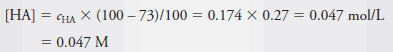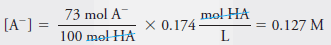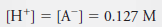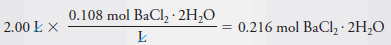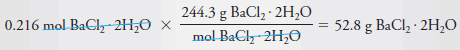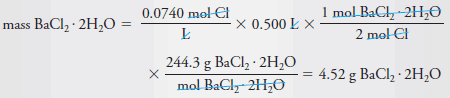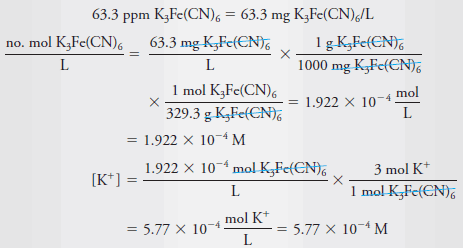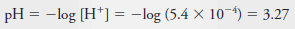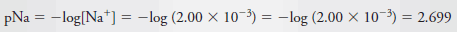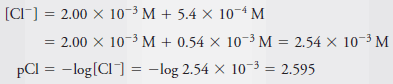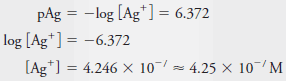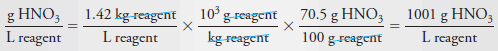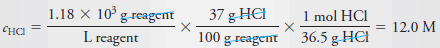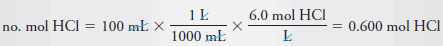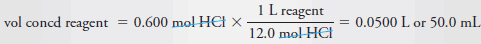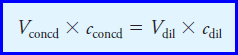Concentration of Solutions: Definitions, Formulas, Solved Problems
– In this subject, we will discuss the Concentration of Solutions Concentration of Solutions (Definitions, Formulas, Solved Problems).

Concentration of Solutions
– For history, measurements and their corresponding units were invented at the local level.
– By necessity of primitive communication and local technology, standards were nearly nonexistent, and conversions among the many systems were difficult.
– The result was many hundreds of distinct ways of expressing concentrations of solutions.
– Fortunately for us, the advent of rapid communications technology and the development of efficient travel have forced the globalization of measurement science and, along with it, the definition of global measurement standards.
– No field has enjoyed more benefit in this regard than chemistry in general and analytical chemistry in particular.
– Even so, we use several methods for expressing concentration.
Ways for Expressing Concentration of Solutions
– In this subject, we describe the four fundamental ways of expressing solution concentration:
(1) molar concentration
(2) percent concentration
(3) solution-diluent volume ratio
(4) p-functions.
(1) Molar Concentration
– The molar concentration cx of a solution of a solute species X is the number of moles of that species that is contained in 1 liter of the solution (not 1 L of the solvent).
– In terms of the number of moles of solute, n, and the volume, V, of solution, we write:
– The unit of molar concentration is molar, symbolized by M, which has the dimensions of mol/L, or mol L-1.
– Molar concentration is also the number of millimoles of solute per milliliter of solution.
Example (1): Calculate the molar concentration of ethanol in an aqueous solution that contains 2.30 g of C2H5OH (46.07 g/mol) in 3.50 L of solution.
Solution:
– To calculate molar concentration, we must find both the amount of ethanol and the volume of the solution.
– The volume is given as 3.50 L, so all we need to do is convert the mass of ethanol to the corresponding amount of ethanol in moles:
– To obtain the molar concentration, cC2H5OH, we divide the amount by the volume. Thus:
– We will see that there are two ways of expressing molar concentration:
- molar analytical concentration
- molar equilibrium concentration.
– The distinction between these two expressions is in whether the solute undergoes a chemical change in the solution process.
(A) Molar Analytical Concentration
– The molar analytical concentration, or for the sake of brevity, just analytical concentration, of a solution gives the total number of moles of a solute in 1 liter of the solution (or the total number of millimoles in 1 mL).
– In other words, the molar analytical concentration specifies a recipe by which the solution can be prepared regardless of what might happen to the solute during the solution process.
– Note that in Example (1), the molar concentration that we calculated is also the molar analytical concentration cC2H5OH = 0.0143 M because the solute ethanol molecules are intact following the solution process.
– In another example, a sulfuric acid solution that has an analytical concentration of cH2SO4= 1.0 M can be prepared by dissolving 1.0 mole, or 98 g, of H2SO4 in water and diluting the acid to exactly 1.0 L.
– As we shall see, there are important differences between the ethanol and sulfuric acid examples.
(B) Molar Equilibrium Concentration
– The molar equilibrium concentration, or just equilibrium concentration, refers to the molar concentration of a particular species in a solution at equilibrium.
– To specify the molar equilibrium concentration of a species, it is necessary to know how the solute behaves when it is dissolved in a solvent.
– For example, the molar equilibrium concentration of H2SO4 in a solution with a molar analytical concentration cH2SO4 = 1.0 M is actually 0.0 M because the sulfuric acid is completely dissociated into a mixture of H+, HSO4–, SO4– ions.
– There are essentially no H2SO4 molecules in this solution.
– The equilibrium concentrations of the ions are 1.01, 0.99, and 0.01M, respectively.
– Equilibrium molar concentrations are usually symbolized by placing square brackets around the chemical formula for the species.
– So, for our solution of H2SO4with an analytical concentration of cH2SO4 = 1.0 M, we write:
Solved Problems on Molar Concentration
Example (2): Calculate the analytical and equilibrium molar concentrations of the solute species in an aqueous solution that contains 285 mg of trichloroacetic acid, Cl3CCOOH (163.4 g/mol), in 10.0 mL (the acid is 73% ionized in water).
Solution:
– As in Example (1), we calculate the number of moles of Cl3CCOOH, which we designate as HA, and divide by the volume of the solution, 10.0 mL, or 0.0100 L. Therefore:
– The molar analytical concentration, cHA, is then:
– In this solution, 73% of the HA dissociates, giving H+ and A–:
– The equilibrium concentration of HA is then 27% of cHA. Thus,
– The equilibrium concentration of A– is equal to 73% of the analytical concentration of HA, that is
– Because 1 mole of H+ is formed for each mole of A–, we can also write:
Example (3): Describe the preparation of 2.00 L of 0.108 M BaCl2 from BaCl2.2H2O (244.3 g/mol).
Solution
– To determine the number of grams of solute to be dissolved and diluted to 2.00 L, we note that 1 mole of the dihydrate yields 1 mole of BaCl2.
– Therefore, to produce this solution we will need:
– The mass of BaCl2.2H2O is then:
– Dissolve 52.8 g of BaCl2.2H2O in water and dilute to 2.00 L.
Example (4): Describe the preparation of 500 mL of 0.0740 M Cl2 solution from solid BaCl2.2H2O (244.3 g/mol).
Solution:
– Dissolve 4.52 g of BaCl2.2H2O in water and dilute to 0.500 L or 500 mL.
(2) Percent Concentration
– Chemists frequently express concentrations in terms of percent (parts per hundred).
– Unfortunately, this practice can be a source of ambiguity because the percent composition of a solution can be expressed in several ways.
– Three common methods are:
Note that:
(1) the denominator in each of these expressions is the mass or volume of solution rather than the mass or volume of the solvent.
(2) the first two expressions do not depend on the units used for weight (mass) as long as the same units are used in the numerator and the denominator.
(3) In the third expression, units must be defined because the numerator and denominator have different units that do not cancel.
(4) Of the three expressions, only weight percent has the advantage of being temperature independent.
– Weight percent is often used to express the concentration of commercial aqueous reagents.
– For example, nitric acid is sold as a 70% (w/w) solution, meaning that the reagent contains 70 g of HNO3 per 100 g of solution (see Example 8).
– Volume percent is commonly used to specify the concentration of a solution prepared by diluting a pure liquid compound with another liquid.
– For example, a 5% (v/v) aqueous solution of methanol usually describes a solution prepared by diluting 5.0 mL of pure methanol with enough water to give 100 mL.
– Weight or volume percent is often used to indicate the composition of dilute aqueous solutions of solid reagents.
– For example, 5% (w/v) aqueous silver nitrate often refers to a solution prepared by dissolving 5 g of silver nitrate in sufficient water to give 100 mL of solution.
– To avoid uncertainty, always specify explicitly the type of percent composition being discussed.
– If this information is missing, the investigator must decide intuitively which of the several types is to be used.
– The potential error resulting from a wrong choice is considerable.
– For example, commercial 50% (w/w) sodium hydroxide contains 763 g NaOH per liter, which corresponds to 76.3% (w/v) sodium hydroxide.
Parts per Million and Parts per Billion
– For very dilute solutions, parts per million (ppm) is a convenient way to express concentration:
– where cppm is the concentration in parts per million.
– The units of mass in the numerator and denominator must agree so that they cancel.
– For even more dilute solutions, 109 ppb rather than 106 ppm is used in the previous equation to give the results in parts per billion (ppb).
– The term parts per thousand (ppt) is also used, especially in oceanography.
Example (5): What is the molar concentration of K+ in a solution that contains 63.3 ppm of K3Fe(CN)6 (329.3 g/mol)?
Solution:
– Because the solution is so dilute, it is reasonable to assume that its density is 1.00 g/mL. therefore:
(3) Solution-Diluent Volume Ratios
– The composition of a dilute solution is sometimes specified in terms of the volume of a more concentrated solution and the volume of solvent used in diluting it.
– The volume of the former is separated from that of the latter by a colon.
– Thus, a 1:4 HCl solution contains four volumes of water for each volume of concentrated hydrochloric acid.
– This method of notation is frequently ambiguous in that the concentration of the original solution is not always obvious to the reader.
– Moreover, under some circumstances, 1:4 means diluting one volume with three volumes.
– Because of such uncertainties, you should avoid using solution-diluent ratios.
(4) p-Functions
– Scientists frequently express the concentration of a species in terms of its p-function, or p-value.
– The p-value is the negative logarithm (to the base 10) of the molar concentration of that species. Thus, for the species X:
As shown by the following examples, p-values offer the advantage of allowing concentrations that vary over ten or more orders of magnitude to be expressed in terms of small positive numbers.
Example (6): Calculate the p-value for each ion in a solution that is 2.00 × 10-3 M in NaCl and 5.4 × 10-4 M in HCl.
Solution:
– To obtain pNa, we write:
– The total Cl2concentration is given by the sum of the concentrations of the two solutes:
Example (7): Calculate the molar concentration of Ag+ in a solution that has a pAg of 6.372.
Solution:
Density and Specific Gravity of Solutions
– Density and specific gravity are related terms often found in the analytical literature.
– The density of a substance is its mass per unit volume, and its specific gravity is the ratio of its mass to the mass of an equal volume of water at 4°C.
– Density has units of kilograms per liter or grams per milliliter in the metric system. Specific gravity is dimensionless and so is not tied to any particular system of units. For this reason, specific gravity is widely used in describing items of commerce.
– The following Figure shows the Label from a bottle of reagent-grade hydrochloric acid.
– Note that the specific gravity of the acid over the temperature range of 60° to 80°F is specified on the label:
– Since the density of water is approximately 1.00 g/mL and since we use the metric system throughout this text, we use density and specific gravity interchangeably.
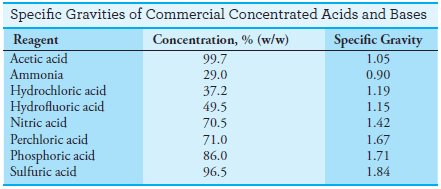
– The specific gravities of some concentrated acids and bases are given in the following Table:
Solved Problems on Concentration
Example (8): Calculate the molar concentration of HNO3 (63.0 g/mol) in a solution that has a specific gravity of 1.42 and is 70.5% HNO3 (w/w).
Solution
Let us first calculate the mass of acid per liter of concentrated solution:
Example (9): Describe the preparation of 100 mL of 6.0 M HCl from a concentrated solution that has a specific gravity of 1.18 and is 37% (w/w) HCl (36.5 g/mol).
Solution
– Proceeding as in Example (8), we first calculate the molar concentration of the concentrated reagent.
– We then calculate the number of moles of acid that we need for the diluted solution.
– Finally, we divide the second figure by the first to obtain the volume of concentrated acid required.
– Thus, to obtain the concentration of the reagent, we write:
– The number of moles HCl required is given by:
– Finally, to obtain the volume of concentrated reagent, we write:
– Therefore, dilute 50 mL of the concentrated reagent to 600 mL.
– The solution to Example (9) is based on the following useful relationship, which we will be using countless times:
– where the two terms on the left are the volume and molar concentration of a concentrated solution that is being used to prepare a diluted solution having the volume and concentration given by the corresponding terms on the right.
– This equation is based on the fact that the number of moles of solute in the diluted solution must equal the number of moles in the concentrated reagent.
– Note that the volumes can be in milliliters or liters as long as the same units are used for both solutions.
Reference: Fundamentals of analytical chemistry / Douglas A. Skoog, Donald M. West, F. James Holler, Stanley R. Crouch. (ninth edition), 2014. USA