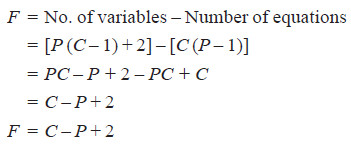Derivation of the phase rule
– Here the derivation of the phase rule for one-component system and two-component system are discussed.
– Consider a heterogeneous system in equilibrium of C components in which P phases are present.
– We have to determine the degrees of freedom of this system i.e., the number of variables which must be arbitrarily fixed in order to define the system completely.
– Since the state of the system will depend upon the temperature and the pressure, these two variables are always there.
– The concentration variables, however, depend upon the number of phases. In order to define the composition of each phase it is necessary to specify the concentration of (C – 1) constituents of each phase, the concentration of the remaining component being determined by difference.
– For P phases, therefore, the total number of concentration variables will be P (C – 1) and these along with the two variables mentioned above viz., temperature and pressure, make the total number of the variables of the system equal to [P (C – 1) + 2].
– On thermodynamic consideration when a system is in equilibrium, the partial molal free energy of each constituent of a phase is equal to the partial molal free energy of the same constituent in every other phase.
– Since the partial molal free energy of the constituents of a phase is a function of the temperature, pressure and (C – 1) concentration variables, it follows that if there is one component in two phases, it is possible to write one equation amongst the variables and if there is one component in three phases, this fact may be written with the help of two equations.
– In general, therefore, when P phases are present, (P – 1) equations are available for each component and for C components, the total number of equations or variables are C (P – 1).
– Since the number of equations is equal to the number of variables, the number of unknown variables or degrees of freedom (F) will be :
Derivation of the phase rule for One-component system
– For a one-component system we can write the phase rule equation as :
F = C – P + 2 = 1 – P + 2 = 3 – P
– Three cases may arise :
Case 1. When only one phase is present
∴ F = 3 – 1 = 2
– Thus the system is bivariant. It can be completely defined by specifying the two variables, temperature and pressure.
– Or that, both the temperature and pressure can be varied independently.
– Therefore a single phase is represented by an area on P, T-graph.
Case 2. When two phases are in equilibrium,
F = 3 – 2 = 1
– The system then has one degree of freedom and is termed monovariant.
– This means that the pressure cannot be changed independently if we change the temperature.
– The pressure is fixed automatically for a given temperature. A two-phase system is depicted by a line on a P, T-graph.
Case 3. When three phases are in equilibrium,
F = 3 – P = 3 – 3 = 0
∴ F = 0
– The system has zero degree of freedom and is termed nonvariant or invariant. This special condition can be attained at a definite temperature and pressure.
– The system is, therefore, defined completely and no further statement of external conditions is necessary.
– A three-phase system is depicted by a point on the P, T-graph. At this point the three phases (solid, liquid, vapour) are in equilibrium and, therefore, it is referred to as the Triple point.
Derivation of the phase rule for Two-component system
– When a single phase is present in a two-component system, the degree of freedom is three,
F = 2 – 1 + 2 = 3
– This means that three variables must be specified in order to describe the condition of the phase.
– Thus in such a system, in addition to pressure and temperature the concentration of one of the components has also to be given.
– For graphic representation of these variables, three coordinate axes at right angles to each other would be required. Therefore the phase diagram obtained would be a solid model.
– For the sake of having simple plane diagrams we generally consider only two variables, the third one being a constant.
– For example, for a solid/liquid equilibrium, the gas phase in usually absent and the effect of pressure on the equilibrium is very small.
– Thus when a two-component system consists of solid and liquid phases only, the effect of pressure may be disregarded.
– Then it is necessary to take into account the remaining variables viz., temperature and concentration.
– Such a solid/liquid system with the gas phase absent is called a condensed system.
– The experimental measurements of temperature and concentration in condensed systems are usually carried out under atmospheric pressure.
– Since the degree of freedom in such a case is reduced by one, we may write the Reduced Phase rule as:
F’ = C – P + 1
– where F’ gives the remaining degrees of freedom of the system.
– The reduced phase rule is more convenient to apply to solid/liquid two-component condensed system.
– Since the only variables for two-component solid/liquid systems are temperature and composition, the phase diagrams for such systems consist of Temperature-Concentration graphs (TC graphs).
 Read Chemistry
Read Chemistry