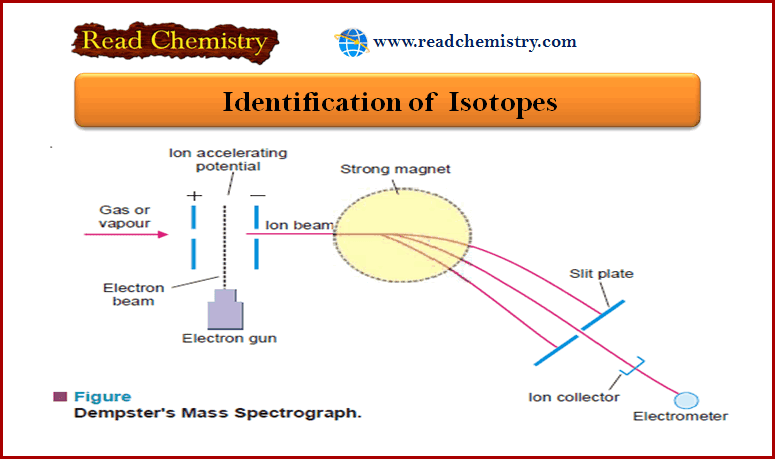
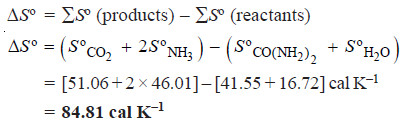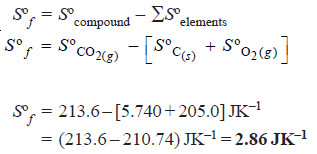Entropy : Definition, Units, Solved Problems

Definition of entropy

– Entropy is a thermodynamic state quantity that is a measure of the randomness or disorder of the molecules of the system.

– The symbol of entropy is S, while the change in disorder accompanying a process from start to completion is represented by ΔS. 

– The entropy of a system is a state function and depends only on the initial and final states of the system.

– The change in entropy, ΔS, for any process is given by the equation,

ΔS = S_final – S_initial

– When S_final > S_initial, ΔS is positive.

– A process accompanied by an increase in entropy tends to be spontaneous.

– Let us consider a molecular system in states A and B (the following figure).

– In state A all the molecules are arranged and highly ordered, while in state B the molecules are present at random and it is highly disordered.

(1) By definition, the entropy of A is low and that of B high.

– Thus an increase of entropy occurs in the change from A to B.

(2) According to the law of chance (probability), A is less probable and B is more probable.

– Therefore, the change from A to B is spontaneous.

(3) From (1) and (2), it follows that the change from A to B which is accompanied by increase of entropy will tend to be spontaneous.

– Hence we can say, in general, that a change in a system which is accompanied by an increase in entropy, tends to be spontaneous.

Statement of The Second law of thermodynamics

– The second law of thermodynamics states that: whenever a spontaneous process takes place, it is accompanied by an increase in the total energy of the universe.

– More specifically, we take the term ‘universe’ to mean the system and the surroundings. Thus,

ΔS_univ = ΔS_syst + ΔS_surr

– The second law, as stated above, tells us that when an irreversible spontaneous process occurs, the entropy of the system and the surroundings increases.

– In other words ΔSuniv > 0. When a reversible process occurs, the entropy of the system remains constant.

– ΔSuniv = 0. Since the entire universe is undergoing spontaneous change, the second law can be most generally and concisely stated as: the entropy of the system is constantly increasing.

Statement of The Third law of thermodynamics

– The entropy of a substance varies directly with temperature.

– The lower the temperature, the lower the entropy.

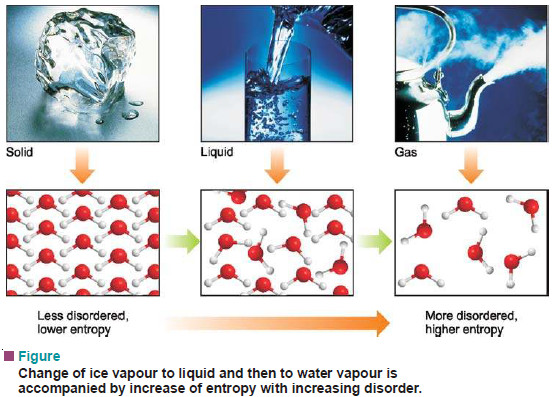
– For example, water above 100ºC at one atmosphere exists as a gas and has higher entropy (higher disorder).

– The water molecules are free to roam about in the entire container.

– When the system is cooled, the water vapour condenses to form a liquid.

– Now the water molecules are confined below the liquid level but still can move about somewhat freely. Thus the entropy of the system has decreased.

– On further cooling, water molecules join together to form ice crystal.

– The water molecules in the crystal are highly ordered and entropy of the system is very low.

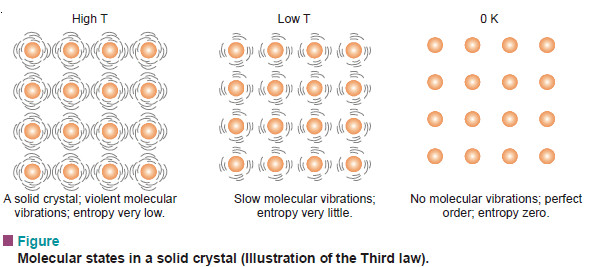
– If we cool the solid crystal still further, the vibration of molecules held in the crystal lattice gets slower and they have very little freedom of movement (very little disorder) and hence very small entropy.

– Finally, at absolute zero all molecular vibration ceases and water molecules are in perfect  order. Now the entropy of the system will be zero.

– This leads us to the statement of the third law of thermodynamics : at absolute zero, the entropy of a pure crystal is also zero. That is, S = 0 at T = 0 K.

Numerical definition of Entropy

– We have discussed the physical definition of entropy.

– But classical thermodynamics does not require a physical explanation of the concept of entropy.

– All that we need is an operational definition so that we can calculate the entropy change of the system and the surroundings.

– In 1850 Clausius introduced a numerical definition of entropy.

– According to him entropy of a system (not undergoing chemical or physical changes), is a constant quantity when there is no communication of heat.

– When heat (q) flows into a system, the entropy increases by q/T .

– Heat flowing out of a system produces a corresponding decrease.

– Thus entropy could be precisely defined as : for a reversible change taking place at a fixed temperature (T), the change in entropy (ΔS) is equal to heat energy absorbed or evolved divided by the temperature (T). That is,

– If heat is absorbed, then ΔS is positive and there will be increase in entropy.

– If heat is evolved, ΔS is negative and there is a decrease in entropy.

Units of Entropy

– As stated above, entropy is equal to heat energy divided by absolute temperature.

– Therefore, it is measured in entropy units (‘eu’) which are calories per degree per mole i.e., cal mol^–1 K^–1.

– In the SI system, the units are joules per mole per degree i.e., J mol^–1 K^–1.

– These are represented by eu.

1 eu = 4.184

Standard Entropy

– From the third law, we know that the entropy of a pure crystal is zero at absolute zero (K) Therefore, it is possible by measurement and calculation to find the actual amount of entropy that a substance possesses at any temperature above 0 K. It is often referred to as absolute entropy.

– The absolute entropy of a substance at 25^ºC (298 K) and one atmosphere pressure is called the standard entropy; S^º.

– The absolute entropy of elements is zero only at 0 K in a perfect crystal, and standard entropies of all substances at any temperature above 0 K always have positive values.

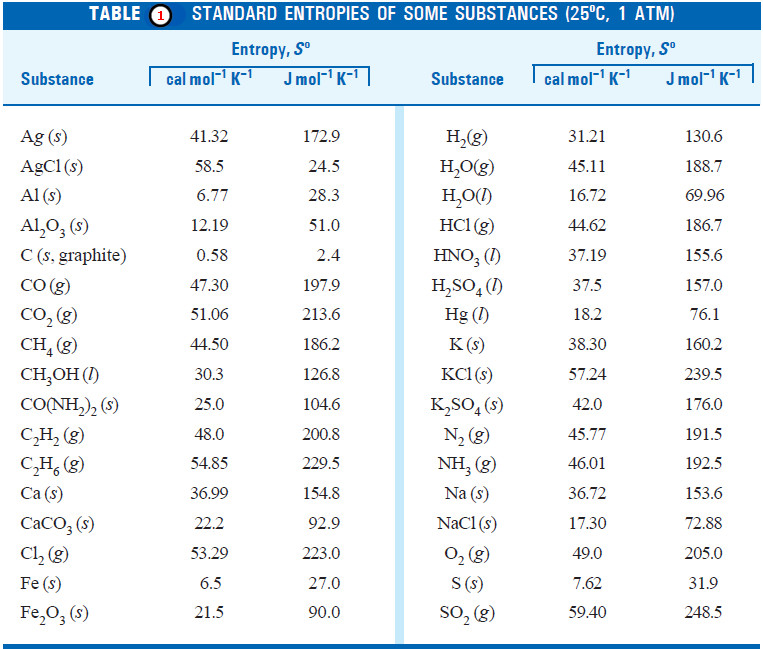
– The standard entropies of a number of elements and compounds are given in Table (1):

– Once we know the entropies of a variety of substances, we can calculate the standard entropy change, ΔSº, for chemical reactions.

ΔS^º = ΣS^º _(products) – ΣS^º _(reactants)

Standard Entropy of Formation

– It is the entropy of formation of 1 mole of a compound from the elements under standard conditions.

– It is denoted ΔS^º_f .

– We can calculate the value of entropy of a given compound from the values of S^º of elements.

S^º_f = S^º _(compound) – ΣS^º _(elements)

Solved Problems 

Problems (1): Urea hydrolyses in the presence of water to produce ammonia and carbon dioxide.

CO(NH₂)_{2 (aq)} + H₂O _(l) ⎯⎯→ CO_{2 (g)} + 2NH_{3 (g)}

What is the standard entropy change for this reaction when 1 mole of urea reacts with water?

The standard entropies of reactants and products are listed below:

Solution:

Problems (2): Calculate the standard entropy of formation, ΔSºf , of CO_{2 (g)}. Given the standard entropies of CO_{2 (g)}, C _(s), O_{2 (g)}, which are 213.6, 5.740, and 205.0 JK^–1 respectively.

Solution:

Physical significance of Entropy

– Entropy is a measure of disorder or randomness of a system.

– The entropy of the system increases if it goes from less orderly state to more orderly state and vice–versa.

– This concept of entropy has led to the conclusion that all substances in their normal crystalline state at absolute zero would be the most ordered state with zero entropy. At this state, all motion ceases.

– In case of a perfect crystal the entropy is zero. This is third law of Thermodynamics

References