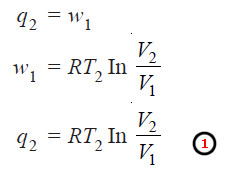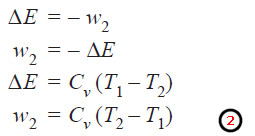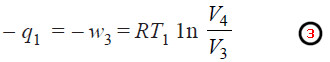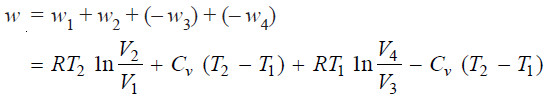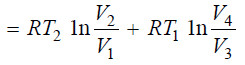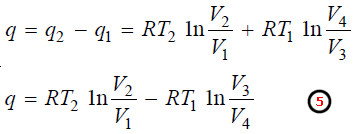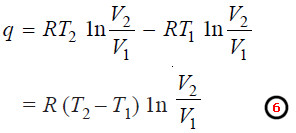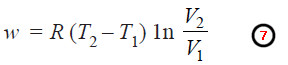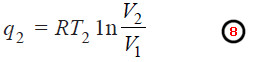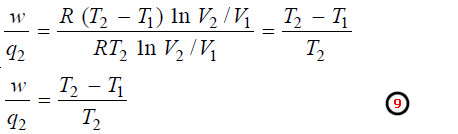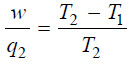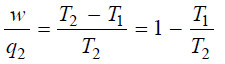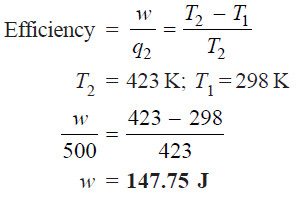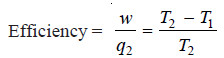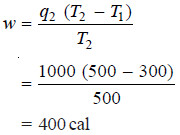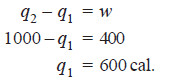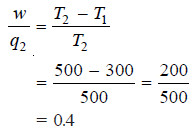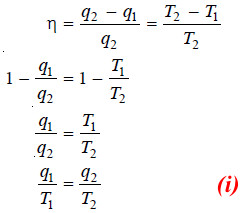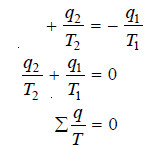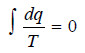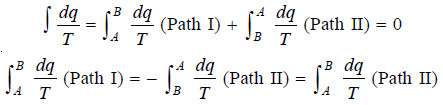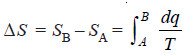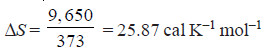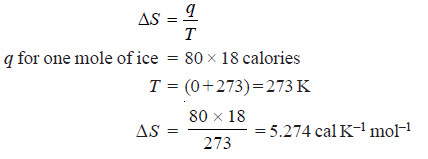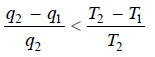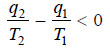Carnot Cycle – Definition, Theorem, Efficiency, Derivation

– In this topic, we will discuss The Carnot Cycle : Definition, Theorem, Efficiency, Derivation and Sovled problems.

The Carnot cycle

– In 1824 Sadi Carnot proposed a theoretical heat engine to show that the efficiency was based upon the temperatures between which it operated.

– Carnot’s imaginary engine could perform a series of operations between temperatures T₁ and T₂, so that at the end of these operations the system was restored to the original state.

– This cycle of processes which occurred under reversible conditions is referred to as the Carnot cycle.

– The medium employed in operating Carnot’s engine was one mole of an ideal gas which could be imagined to be contained in a cylinder fitted with a frictionless piston.

– The Carnot cycle comprises four operations or processes as follows:

(1) Isothermal reversible expansion

(2) Adiabatic reversible expansion

(3) Isothermal reversible compression

(4) Adiabatic reversible compression

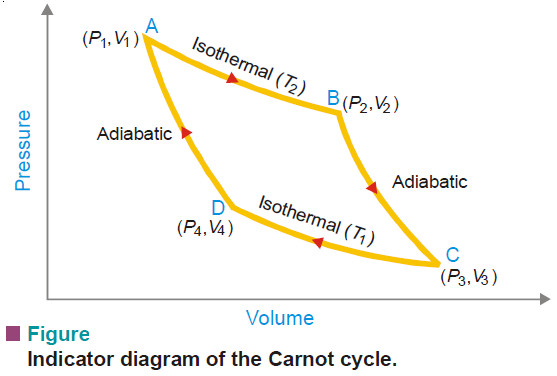
– The above four processes are shown in the indicator diagram of Carnot cycle as follows:

1. First Operation – Isothermal Reversible Expansion

– Let T₂, P₁ and V₁ be the temperature, pressure and volume respectively of the gas enclosed in the cylinder initially.

– The cylinder is placed in the heat reservoir at the higher temperature (T₂).

Now the gas is allowed to expand isothermally and reversibly so that the volume increases from V₁ to V₂.

– AB represents the path of the process in the diagram.

– Work done. Since the process in operation 1 is isothermal, ΔE = 0.

– If q₂ be the heat absorbed by the system and w₁ the work done by it, according to the first law equation (ΔE = q – w),

2. Second Operation – Adiabatic Reversible Expansion

– The gas at B is at a temperature T₂ and has volume V₂ under the new pressure P₂.

– The gas is now allowed to expand reversibly from volume V₂ to V₃ when the temperature drops from T₂ to T₃ (along BC).

– Work done. Since this step is adiabatic, q = 0. If w₂ be the work done, according to the first law equation (Δ E = q – w),

3. Third Operation – Isothermal Reversible Compression

– Now the cylinder is placed in contact with a heat reservoir at a lower temperature, T₁.

– The volume of the gas is then compressed isothermally and reversibly from V₃ to V₄ (represented by CD in diagram).

Work done. During compression, the gas produces heat which is transferred to the low temperature reservoir. Since the process takes place isothermally, ΔE = 0.

– If q₁ is the heat given to the reservoir and w₃ the work done on the gas, using proper signs for q and w, we have:

4. Fourth Operation – Adiabatic Reversible Compression

– The gas with volume V₄ and temperature T₁ at D is compressed adiabatically (along DA) until it regains the original state.

– That is, the volume of the system becomes V₁ and its temperature T₂.

– Work done. In this step work is done on the system and, therefore, bears the negative (–) sign.

– If it is denoted by w₄, we can write

Net Work Done in One Cycle

– Adding up the work done (w) in all the four operations of the cycle as shown in equations (1), (2), (3) and (4), we have:

Net Heat Absorbed in One Cycle

– If q is the net heat absorbed in the whole cycle.

q = q₂ – q₁

– where q₂ is heat absorbed by the system in operation 1 and q1 is the heat transferred to the sink reservoir.

– From (1) and (3):

– According to the expression governing adiabatic changes,

– Therefore, substituting the value of V₃/V₄ in equation (5), the value of net heat may be given as:

Calculation of Thermodynamic Efficiency

– Since the total work done in a cycle is equal to net heat absorbed, from (6) we can write:

– The heat absorbed, q₂, at higher temperature T₂ is given by equation (1),

– Dividing (7) by (8):

– The factor w/q₂ is called thermodynamical efficiency.

– It is denoted by η and gives the fraction of the heat taken from the high-temperature reservoir which it is possible to convert into work by a heat engine.

– Therefore, the efficiency of a Carnot engine, the most ideal of all engines, is limited by the operating temperatures of the engine.

– The larger the temperature difference (T₂ – T₁) between the high and the low temperature reservoirs, the more the heat converted to work by the heat engine.

– For a given temperature of the high-temperature reservoir, the lower the temperature of the sink, the greater will be the efficiency of the machine.

– Similarly, for a given temperature of the sink, the efficiency will be increased by using a high temperature of the source reservoir.

Carnot Theorem

– We have shown above that:

– This result deduced for a perfect gas depends upon the temperature limits between which the cycle  operates. It is independent of all other factors.

– Thus Carnot stated an important relation known as the Carnot theorem.

– Carnot theorem states that : every perfect engine working reversibly between the same temperature limits has the same efficiency, whatever be the working substance.

More statement of the Second law

From equation (9):

– Evidently w/q₂ is less than 1, or q₂ is greater than w.

– This means that heat transferred by a spontaneous process is never completely converted into work (If so, w/q₂ would be 1). This leads to another statement of the Second law (Lord Kelvin).

– It is impossible to take heat from a hotter reservoir and convert it completely into work by a cyclic process without transferring a part of heat to a cooler reservoir.

– This statement recognises the fact that heat engines could never be 100% efficient, since some heat must be returned to a low-temperature reservoir. Another statement of the Second law was given by Clausius.

– It is impossible for a cyclic process to transfer heat from a body at a lower temperature to one at higher temperature without at the same time converting some work to heat.

– This statement recognises that heat flows spontaneously from hot objects to cold objects and to get it flow in the opposite direction, we have to expend some work.

Solved Problems on Carnot Cycle

Problem (1): An engine operating between 150^ºC and 25^ºC takes 500 J heat from a high temperature reservoir. Assuming that there are no frictional losses, calculate the work that can be done by this engine.

Solution:

From equation (9):

Problem (2): The boiling point of water at a pressure of 50 atmosphere is 265^ºC. Compare the theoretical efficiencies of a steam engine operating between the boiling point of water at (i) 1 atmosphere (ii) 50 atmosphere, assuming the temperature of the sink to be 35^ºC in each case.

Solution:

Problem (3): If a Carnot engine operating between two heat reservoirs at 227^ºC and 27^ºC absorbs 1000 calories from the 227^ºC reservoir per cycle, how much heat is discharged into the 27^ºC reservoir and how much work is done per cycle ? What is the efficiency of the cycle ?

Solution:

(a) We know that:

– The work done per cycle is 400 cal

(b) The heat from the high-temperature reservoir (q₂) minus the heat discharged into the lowtemperature reservoir (q₁) is converted into work (w). Thus,

(c) Efficiency :

– Therefore, efficiency of the engine is 0.4

Derivation of entropy from Carnot cycle

– Because processes cannot be 100% efficient, a term to describe the energy available for doing useful work becomes necessary.

– Although we have discussed the concept of entropy already, its classical derivation deserves attention.

– In a Carnot cycle, q₂ has a positive value and q1 has a negative value, since former is taken up at a higher temperature and the latter is given out at the lower temperature.

– Thus thermodynamic efficiency may be expressed as

– using sign convention, heat absorbed (i.e., q₂) is given the +ve sign and heat lost (i.e. q₁) is given the – ve sign. Equation (i) becomes:

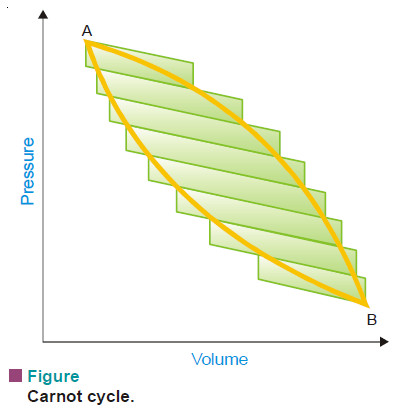
– Any reversible cycle may be regarded as made up of a number of Carnot cycles.

– Consider, for example, the cycle represented in the following Fig. by the closed curve ABA.

– Imagine a series of isothermal and adiabatic curves drawn across the diagram so that a number of Carnot cycles are indicated.

– Starting at A and going through all the cycles successively from A to B, it can be shown that all paths inside the diagram cancel each other leaving only zigzag outer path.

– The larger the number of cycles taken in this manner, the closer will the resultant path correspond to ABA which represents the reversible cycle under consideration.

– The reversible cycle can, therefore, be regarded as being made up of an infinite number of Carnot cycles, for each of which the sum of the two q/T terms involved is zero i.e.,

– For the reversible cycle ABA comprising a series of Carnot cycles, therefore, the above expression takes the form

– and for an infinite number of Carnot cycles

– Since the cycle is performed in two steps, viz., from A to B and then back from B to A, we have:

– It is evident, therefore, that both these integrals are independent of the path taken from A to B.

– Both depend upon the value of some function at A and the same function at B. This function is called entropy (S).

– Let S_B be the entropy at the state B and SA in the state A.

– Then, the increase in entropy, ΔS, is given by the expression:

– and for each infinitesimally small change:

– Like ΔE and ΔH, ΔS is dependent only on the state of the system and can be calculated if the substance can be brought reversibly from one state to the other. It is independent of the path taken.

Solved Problems

Problem (4): Calculate the entropy change in the evaporation of 1 mole of water at 100ºC. Latent heat of evaporation of water is 9,650 cals per mole.

Solution:

– Entropy change on the evaporation of 1 mole of water is obtained by dividing the latent heat of evaporation of 1 mole of water by the absolute temperature

Problem (5): Calculate the increase in entropy when one gram molecular weight of ice at 0^ºC melts to form water. Latent heat of fusion of ice = 80 calories.

Solution:

Entropy Change an irreversible Carnot cycle

– The efficiency of an irreversible Carnot cycle is always less than that of a reversible one operating between the same two temperatures

– where q₂ is the heat absorbed at temperature T2 and q1 is the heat returned at temperature T1.

– In other words  for an irreversible cycle is always less than zero and the entropy of the final state is always greater than that of the initial state.

– As most of the processes going on in nature are spontaneous and irreversible, it has been said that “the entropy of the universe always tends towards a maximum”.

References