Water system, Phase diagram of Water
The Water system
– Under normal conditions the Water system is a three-phase, one-component system.
– The three phases involved are liquid water, ice, water vapour.
– All these phases can be represented by one chemical entity H2O and hence one component of the system.
– The number of phases which can exist in equilibrium any time depends on the conditions of temperature and pressure.
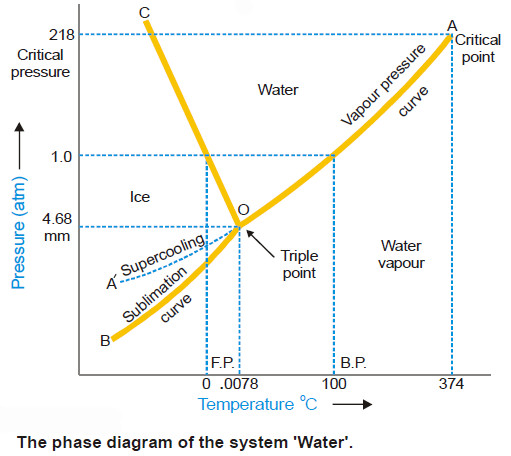
– The phase diagram or PT-graph of the system/ water/ice/vapour is shown in the following Figure.
– The salient features of the phase diagram are listed below.
(1) The Curves OA, OB, OC
(2) The Triple Point O
(3) The Areas AOC, AOB, BOC
– Let us proceed to discuss the significance of each of these features.
(1) The Curves OA, OB, OC
– These three curves meet at the point O and divide the diagram into three regions or areas.
Curve OA, the Vapour Pressure curve of Water.
– It represents the vapour pressure of liquid water at different temperatures.
– The two phases water and water vapour coexist in equilibrium along this curve.
– The curve OA terminates at A, the critical point (218 atm, temp. 374ºC) when the liquid and vapour are indistinguishable from each other and there is left one phase only.
– When the vapour pressure is equal to one-atmosphere, the corresponding temperature, as indicated on the phase diagram is the boiling point (100ºC) of water.
Curve OB, the Sublimation curve of Ice
– It shows the vapour pressure of solid ice at different temperatures.
– The two phases solid ice and vapour coexist in equilibrium along this curve.
– At the lower limit the curve OB terminates at absolute zero (– 273ºC) where no vapour exists.
Curve OC, the Fusion curve of Ice
– It depicts the effect of pressure on the melting point of ice.
– Here ice and water coexist in equilibrium.
– The fact that OC slopes to the left indicates that the melting point of ice decreases with increase of pressure.
– Since ice melts with decrease in volume by Le Chatelier’s principle the melting point is lowered by an increase of pressure.
– It may be noted that the 1.0 atmosphere line meets the fusion curve at 0ºC which is the normal melting point of ice.
– Along the curves OA, OB, OC there are two phases in equilibrium and one component. Therefore,
F = C – P + 2 = 1 – 2 + 2 = 1
– Hence each two-phase system :
- water/water vapour represented by OA
- ice/water vapour represented by OB
- ice/water represented by OC
has one degree of freedom i.e., is monovariant.
(2) The Triple point (O)
The curves OA, OB and OC meet at the triple point ‘O’ where all the three phases liquid water/ ice/vapour are in equilibrium.
– This occurs at 0.0076ºC and vapour pressure 4.58 mm Hg. Since there are three phases and one component, we have
F = C– P + 2 = 1 – 3 + 2 = 0
i.e., the system at the triple point is nonvariant.
– Thus if either pressure or temperature is changed, the three phases would not exist and one of the phases would disappear.
(3) Area AOC, AOB, BOC
The areas or regions between the curves show the conditions of temperature and pressure under which a single phase–ice, water or vapour is capable of stable existence. Thus,
– Area AOC represents conditions for the one-phase system water.
– Area AOB represents conditions for the one-phase system water vapour.
– but Area BOC represents conditions for the one-phase system ice.
In all the three areas there being one-phase and one-component, we have:
F = C – P + 2 = 1 – 1 + 2 = 2
– Thus each system water, water vapour, or ice has 2 degrees of freedom i.e., the system is
bivariant.
(4) Metastable system : Supercooled Water/Vapour System
– The vapour pressure curve of water AO can be continued past the triple point as shown by the dashed line OA’.
– That is, water can be supercooled by carefully eliminating solid particles.
– The supercooled water/vapour system is metastable (unstable).
– It at once reverts to the stable system ice/vapour on the slightest disturbance or introducing a crystal of ice.