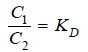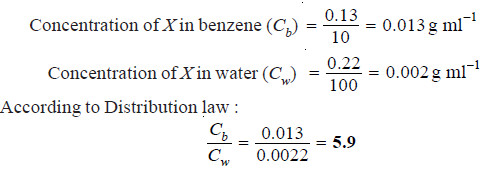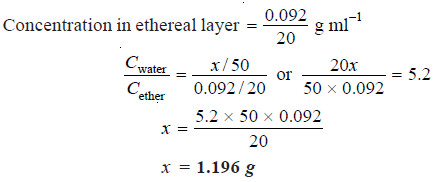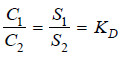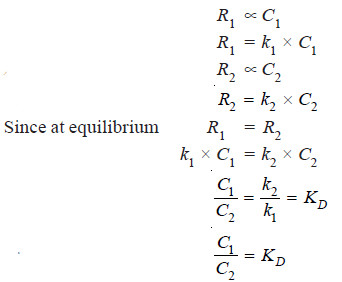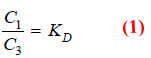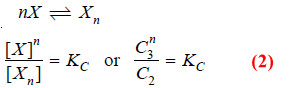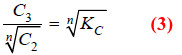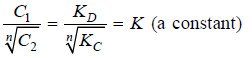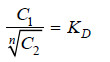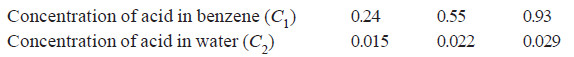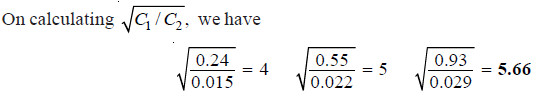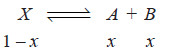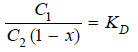Nernst’s Distribution Law + Solved problems
Introduction to Nernst’s Distribution Law
– In this topic Nernst’s Distribution Law wlll be discussed
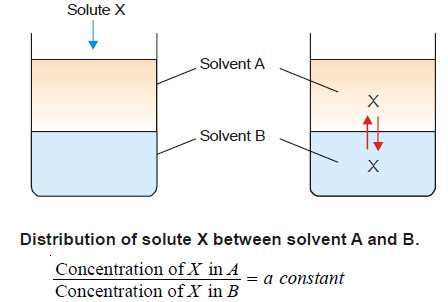
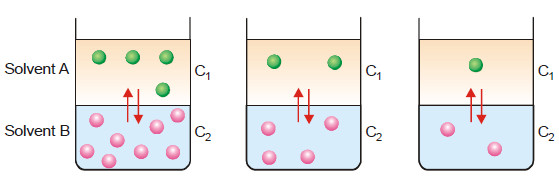
– If we take two immiscible solvents A and B in a beaker, they form separate layers.
– When a solute X which is soluble in both solvents is added, it gets distributed or partitioned between them.
– Molecules of X pass from solvent A to B and from solvent B to A.
– Finally a dynamic equilibrium is set up.
– At equilibrium, the rate, at which molecules of X pass from one solvent to the other is balanced.
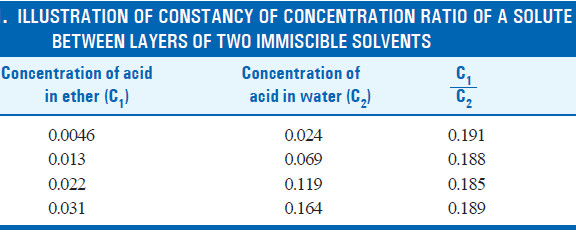
– For example, the following results from the distribution of succinic acid between ether and water illustrate the constancy of the ratio of the concentrations in each layer.
Statement of Nernst’s Distribution Law
– Nernst (1891) studied the distribution of several solutes between different appropriate pairs of solvents.
– He gave a generalization which governs the distribution of a solute between two non-miscible solvents.
– This is called Nernst’s Distribution law (or Nernst’s Partition law) or simply Distribution law or Partition law.
If a solute X distributes itself between two immiscible solvents A and B at constant temperature and X is in the same molecular condition in both solvents,
If C1 denotes the concentration of the solute in solvent A and C2 the concentration in solvent B, Nernst’s Distribution law can be expressed as:
The constant KD (or simply K) is called the Distribution coefficient or Partition coefficient or Distribution ratio.
Solved problems on Nernst’s Distribution Law
Solved problem (1):
A solid X is added to a mixture of benzene and water. After shaking well and allowing to stand, 10 ml of the benzene layer was found to contain 0.13 g of X and 100 ml of water layer contained 0.22 g of X. Calculate the value of distribution coefficient.
Solution:
Solved problem (2):
In the distribution of succinic acid between ether and water at 15ºC, 20 ml of the ethereal layer contains 0.092 g of the acid. Find out the weight of the acid present in 50 ml of the aqueous solution in equilibrium with it if the distribution coefficient for succinic acid between water and ether is 5.2.
Solution:
Let the weight of succinic acid in aqueous layer be x g
Concentration in aqueous layer = x /50 g ml-1
Solved problem (3):
An aqueous solution of succinic acid at 15ºC, containing 0.07 g in 10 ml is in equilibrium with an ethereal solution which has 0.013 g in 10 ml. The acid has its normal molecular weight in both the solvents. What is the concentration of the ethereal solution which is in equilibrium with an aqueous solution containing 0.024 g in 10 ml?
Solution:
Solubilities and Distribution Law
– When a solute is shaken with two non-miscible solvents, at equilibrium both the solvents are saturated with the solute.
– Since the solubility also represents concentration, we can write the distribution law as:
– where S1 and S2 are the solubilities of the solute in the two solvents.
– Hence knowing the value of the Distribution coefficient (KD) and the solubility of solute in one of the solvents, the solubility of solute in the second solvent can be calculated.
Solved problem (4):
At 25º C an aqueous solution of iodine containing 0.0516 g litre–1 is in equilibrium with a carbon tetrachloride (CCl4) solution containing 4.412 g litre–1. The solubility of iodine in water at 25ºC is 0.34 g litre–1. Find the solubility of iodine in carbon tetrachloride.
Solution:
(a) To find the value of KD
Concentration of I2 in water (CH2O) = 0.0516 g litre–1
Concentration of I2 in CCl4 (CCCl4) = 4.412 g litre–1
Explanation of Distribution Law
– This is an equilibrium law. When the distribution of the solute X has reached dynamic equilibrium, the rate (R1) at which molecules of X pass from solvent A to B is proportional to its concentration (C1) in A.
– The rate (R2) at which molecules of X pass from solvent B to A is proportional to its concentration (C2) in B.
– Also, at equilibrium, the rate of migration of solute from one solvent to the other is equal.
Thus we have,
– This is the Nernst’s Distribution law equation.
– Since k1 and k2 are constants at the same temperature, the distribution coefficient KD is also constant if temperature is fixed.
Limitations of Distribution Law
The conditions to be satisfied for the application of the Nernst’s Distribution law are :
(1) Constant temperature. The temperature is kept constant throughout the experiment.
(2) Same molecular state. The molecular state of the solute is the same in the two solvents. The law does not hold if there is association or dissociation of the solute in one of the solvents.
(3) Equilibrium concentrations. The concentrations of the solute are noted after the equilibrium has been established.
(4) Dilute solutions. The concentration of the solute in the two solvents is low. The law does
not hold when the concentrations are high.
(5) Non-miscibility of solvents. The two solvents are non-miscible or only slightly soluble in each other. The extent of mutual solubility of the solvents remains unaltered by the addition of solute to them.
How is distribution law modified by change in molecular state?
– It was pointed out by Nernst that C1/C2 is constant only if the solute exists as simple molecules in the two solvents.
– If the solute undergoes association or dissociation in one of the solvents, it is found that C1/C2 is not constant.
– In these cases, distribution law applies only to that part of the solute which is present as simple molecules.
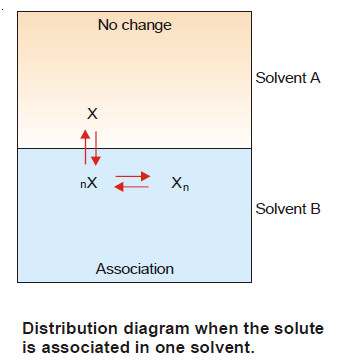
(1) When Solute undergoes Association
– Suppose the solute is present as simple molecules X in solvent A. In solvent B, n molecules of X associate to form Xn molecules.
– Assuming that a few single molecules X are also present in solvent B the equilibria that exist in the two solvents are shown :
Let C1 be concentration of X in solvent A.
C3 be concentration of X in solvent B.
C2 be concentration of Xn in solvent B.
– Applying distribution law to the equilibrium
X in solvent A ↔ X in solvent B
we have:
Applying Mass Law to the chemical equilibrium:
Taking nth root on both sides in equation (2)
Dividing equation (1) by (3)
Thus when association occurs in one solvent, the distribution equation is modified as:
Since the solute exists largely as associated molecules, the total concentration of X determined experimentally in solvent B is taken as the concentration of the associated molecules Xn.
Solved problem (5):
When benzoic acid was shaken with mixtures of benzene and water at constant temperature, the following results were obtained:
Comment on the results.
Solution:
Calculating the ratio C1/C2 for each case;
Thus the distribution coefficient is not constant. Therefore, benzoic acid does not exist as
single molecules in both solvents.
– The constant value of partition coefficient now arrived at, suggests that benzoic acid is associated into double molecules in the benzene layer.
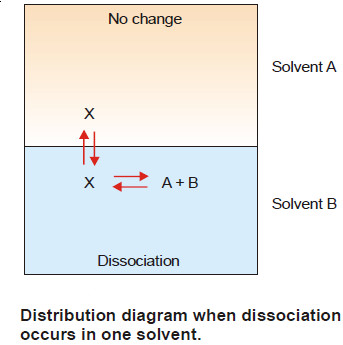
(2) When Solute undergoes Dissociation
– Suppose the solute is present as normal molecules X in solvent A and it dissociates into A + B in solvent B.
– The equilibria set up in the two solvents are shown in Fig.
– Let C1 be the concentration of X in solvent A and C2 the total concentration of X (dissociated and undissociated) in solvent B.
– If the degree of dissociation in solvent B is x,
– Hence the concentration of the undissociated (or normal) molecules in solvent B is C2 (1 – x).
Applying distribution law to normal molecules in the two solvents
– This is the modified distribution law equation when there is dissociation in one of the solvents.
– A case of this type arises in the distribution of a weak acid (e.g., succinic acid or oxalic acid) between ether and water.
– C1 and C2 can be determined by direct titration of the two layers against standard alkali solution.
– The value of x can be found by measuring electrical conductance of solution in solvent B.