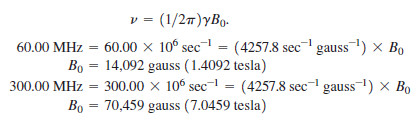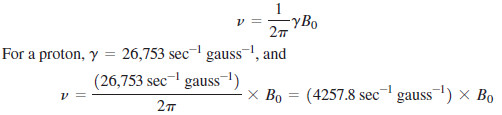NMR – Theory of Magnetic Nuclear Resonance
Introduction to NMR
– Nuclear magnetic resonance spectroscopy (NMR) is the most powerful tool available for organic structure determination.
– Like infrared spectroscopy, NMR can be used with a very small sample, and it does not harm the sample.
– The NMR spectrum provides a great deal of information about the structure of the compound, and many structures can be determined using only the NMR spectrum.
– More commonly, however, NMR spectroscopy is used in conjunction with other forms of spectroscopy and chemical analysis to determine the structures of complicated organic molecules.
– NMR is used to study a wide variety of nuclei, including 1H, 13C, 15N, 19F, and 31P.
Organic chemists find proton (1H) and carbon-13 (13C) to be most useful because hydrogen and carbon are major components of organic compounds.
– Historically, NMR was first used to study protons (the nuclei of hydrogen atoms), and proton magnetic resonance (1H NMR) spectrometers have been the most common.
– Nuclear magnetic resonance is assumed to mean “proton magnetic resonance” unless a different nucleus is specified.
We begin our study of NMR with 1H NMR and conclude with a discussion of 13C NMR.
Theory of Magnetic Nuclear Resonance: NMR Theory
– A nucleus with an odd atomic number or an odd mass number has a nuclear spin that can be observed by the NMR spectrometer.
– A proton is the simplest nucleus, and its odd atomic number of 1 implies it has a spin.
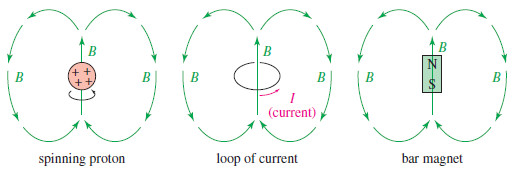
– We can visualize a spinning proton as a rotating sphere of positive charge (Figure).
– This movement of charge is like an electric current in a loop of wire. It generates a magnetic field (symbolized by B), called the magnetic moment, that looks like the field of a small bar magnet.
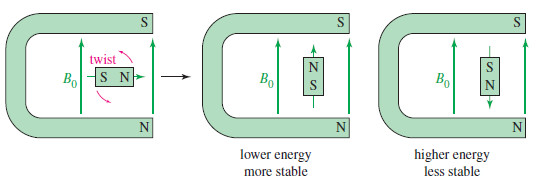
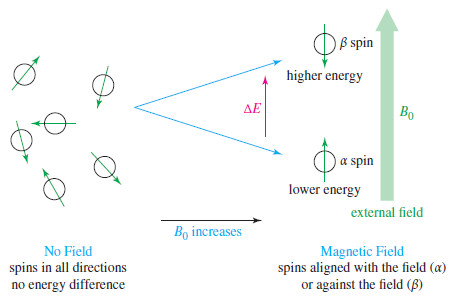
– When a small bar magnet is placed in the field of a larger magnet (Figure), it twists to align itself with the field of the larger magnet—a lower energy arrangement than an orientation against the field. The same effect is seen when a proton is placed in an external magnetic field (B0)as shown here.
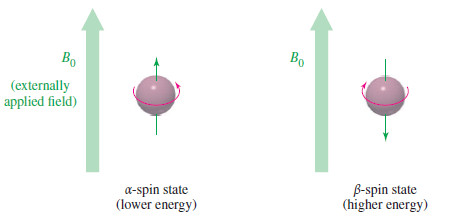
– Quantum mechanics requires the proton’s magnetic moment to be aligned either with the external field or against the field.
– The lower-energy state with the proton aligned with the field is called the alpha-spin (α-spin) state.
– The higher-energy state with the proton aligned against the external magnetic field is called the beta-spin (β-spin) state.
– In the absence of an external magnetic field, proton magnetic moments have random orientations.
– When an external magnetic field is applied, each proton in a sample assumes the state or the state. Because the state is lower in energy, there are more α spins than β spins.
– In a strong magnetic field, the energy difference between the two spin states is larger than it is in a weaker field.
– In fact, the energy difference is proportional to the strength of the magnetic field, as expressed in the equation
where:
ΔE = energy difference between a and b states
h = Planck’s constant
B0 = strength of the external magnetic field
γ = gyromagnetic ratio, 26,753 sec-1 gauss-1 for a proton
– The gyromagnetic ratio (γ) is a constant that depends on the magnetic moment of the nucleus under study.
– Magnetic fields are measured in gauss; for example, the strength of the earth’s magnetic field is about 0.57 gauss.
– The SI unit for magnetic field is the tesla (T), which is simply 10,000 gauss.
The energy difference between a proton’s two spin states is small. For a strong external magnetic field of 25,000 gauss (2.5 T), it is only about 10-5 kcal/mol (4 × 10-5 kj/mol) Even this small energy difference can be detected by NMR.
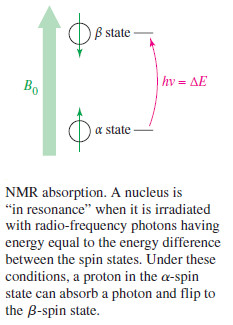
– When a proton interacts with a photon with just the right amount of electromagnetic energy, the proton’s spin can flip from α to β or from β to α nucleus aligned with the field can absorb the energy needed to flip and become aligned against the field.
– When a nucleus is subjected to the right combination of magnetic field and electromagnetic radiation to flip its spin, it is said to be “in resonance”, and its absorption of energy is detected by the NMR spectrometer. This is the origin of the term “nuclear magnetic resonance.”
– A photon’s energy is given by E = hv meaning that the energy, E, is proportional to v, the frequency of the electromagnetic wave.
– This equation can be combined with the equation for the energy difference between the spin states:
– Rearranging to solve for shows that the resonance frequency is proportional to the applied magnetic field (B0) and the gyromagnetic ratio (γ):
– For the fields of currently available magnets, proton resonance frequencies occur in the radio-frequency (RF) region of the spectrum.
– NMR spectrometers are usually designed for the most powerful magnet that is practical for the price range of the spectrometer, and the radio frequency needed for resonance is calculated based on the field.
– A more powerful magnet makes ΔE larger and more easily detected, and it increases the frequency difference between signals, giving spectra that are more clearly resolved and easier to interpret.
– In the past, the most common operating frequency for student spectrometers has been 60 MHz (megahertz; 1 million cycles per second), corresponding to a magnetic field of 14,092 gauss.
– Higher-resolution instruments commonly operate at frequencies of 200 to 600 MHz (and higher), corresponding to fields of 46,972 to 140,918 gauss.
Solved Problem
Calculate the magnetic fields that correspond to proton resonance frequencies of 60.00 MHz and 300.00 MHz.
Solution
We substitute into the equation: