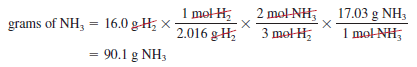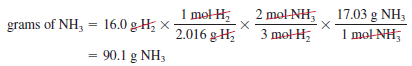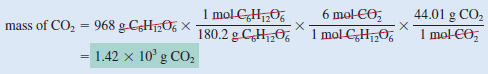Amounts of Reactants and Products
– In this subject, we will discuss Amounts of Reactants and Products
Amounts of Reactants and Products
– A basic question raised in the chemical laboratory is (How much product will be formed from specific amounts of starting materials (reactants)?) Or in some cases, we might ask the reverse question: (How much starting material must be used to obtain a specific amount of product?)
– To interpret a reaction quantitatively, we need to apply our knowledge of molar masses and the mole concept.
– Stoichiometry is the quantitative study of reactants and products in a chemical reaction.
– Whether the units given for reactants (or products) are moles, grams, liters (for gases), or some other units, we use moles to calculate the amount of product formed in a reaction.
– This approach is called the mole method, which means simply that the stoichiometric coefficients in a chemical equation can be interpreted as the number of moles of each substance.
Examples for indicating Amounts of Reactants and Products
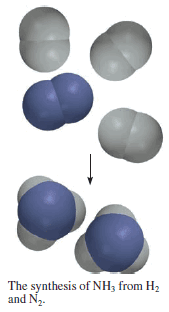
Synthesis of Ammonia
– For example, industrially ammonia is synthesized from hydrogen and nitrogen as follows:
– The stoichiometric coefficients show that one molecule of N2 reacts with three molecules of H2 to form two molecules of NH3.
– It follows that the relative numbers of moles are the same as the relative number of molecules:
– Thus, this equation can also be read as (1 mole of N2 gas combines with 3 moles of H2 gas to form 2 moles of NH3 gas.)
– In stoichiometric calculations, we say that 3 moles of H2 are equivalent to 2 moles of NH3, that is,
– where the symbol ≈ means (stoichiometrically equivalent to) or simply (equivalent to.)
– This relationship enables us to write the conversion factors
– Similarly, we have 1 mol N2 ≈ 2 mol NH3, and 1 mol N2 ≈ 3 mol H2.
6.0 moles of H2 react completely with N2 to form NH3
– Let’s consider a simple example in which 6.0 moles of H2 react completely with N2 to form NH3.
– To calculate the amount of NH3 produced in moles, we use the conversion factor that has H2 in the denominator and write:
– Now suppose 16.0 g of H2 reacts completely with N2 to form NH3. How many grams of NH3 will be formed?
– To do this calculation, we note that the link between H2 and NH3 is the mole ratio from the balanced equation.
– So we need to first convert grams of H2 to moles of H2, then to moles of NH3, and finally to grams of NH3.
– The conversion steps are:
(1) we convert 16.0 g of H2 to the number of moles of H2, using the molar mass of H2 as the conversion factor:
(2) we calculate the number of moles of NH3 produced
(3) we calculate the mass of NH3 produced in grams using the molar mass of NH3as the conversion factor:
– These three separate calculations can be combined in a single step as follows:
– Similarly, we can calculate the mass in grams of N2 consumed in this reaction. The conversion steps are:
– By using the relationship 1 mol N2 ≈ 3 mol H2, we write
Stoichiometric Calculations
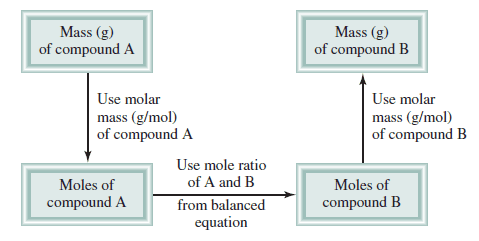
– The following Figure shows the steps involved in stoichiometric calculations using the mole method.
First: convert the quantity of reactant A (in grams or other units) to the number of moles.
Next: use the mole ratio in the balanced equation to calculate the number of moles of product B formed.
Finally: convert moles of product to grams of product.
Solved Problems on Amounts of Reactants and Products
Problem (1)
The food we eat is degraded, or broken down, in our bodies to provide energy for growth and function. A general overall equation for this very complex process represents the degradation of glucose (C6H12O6) to carbon dioxide (CO2) and water (H2O):
If 968 g of C6H12O6is consumed by a person over a certain period, what is the mass of CO2 produced
Strategy:
– Looking at the balanced equation, how do we compare the amount of C6H12O6 and CO2?
– We can compare them based on the mole ratio from the balanced equation.
– Starting with grams of C6H12O6, how do we convert to moles of C6H12O6?
– Once moles of CO2 are determined using the mole ratio from the balanced equation, how do we convert to grams of CO2?
Solution
– We follow the preceding steps and Figure (1).
Step (1): The balanced equation is given in the problem.
Step(2): To convert grams of C6H12O6 to moles of C6H12O6, we write
Step (3): From the mole ratio, we see that 1 mol C6H12O6 ≈ 6 mol CO2. Therefore, the number of moles of CO2 formed is
Step (4): Finally, the number of grams of CO2 formed is given by
– After some practice, we can combine the conversion steps
into one equation:
Problem (2)
All alkali metals react with water to produce hydrogen gas and the corresponding alkali metal hydroxide. A typical reaction is that between lithium and water:
How many grams of Li are needed to produce 7.79 g of H2?

Strategy:
– The question asks for the number of grams of reactant (Li) to form a specific amount of product (H2).
– Therefore, we need to reverse the steps shown in Figure (1).
– From the equation, we see that 2 mol Li ≈ 1 mol H2.
Solution:
– The conversion steps are
– Combining these steps into one equation, we write
Check:
– There are roughly 4 moles of H2 in 7.79 g H2, so we need 8 moles of Li.
– From the approximate molar mass of Li (7 g), does the answer seem reasonable?
Reference: Organic chemistry / T.W. Graham Solomons, Craig B.Fryhle, Scott A. Snyder, / ( eleventh edition) / 2014.