Distribution of Electrons in Orbitals

– In this subject, we will discuss the Distribution of Electrons in Orbitals according to Hund’s Rule.

Energy Distribution and Orbitals

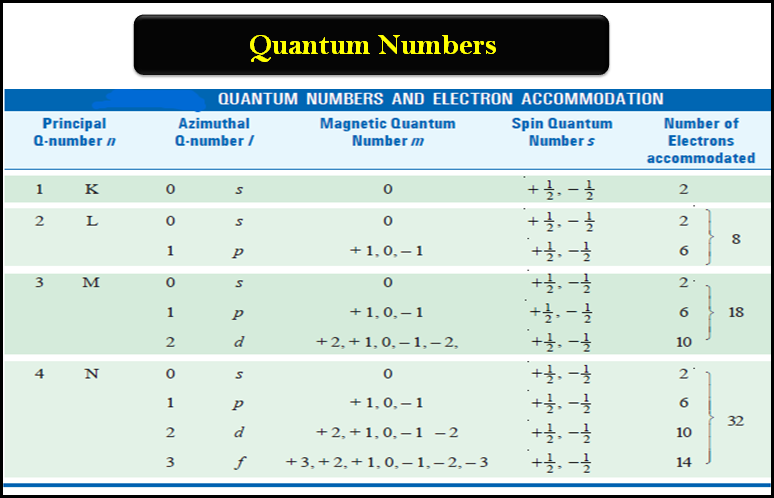
– In our earlier discussion, we have seen that the energy of an electron is determined by the first two quantum numbers (n) and (l), while the other two specify the orientation of the electron orbital in space and the spin.

– As we discuss the distribution of energy of the orbitals, the following two cases may arise:

(a) Hydrogen and Hydrogen-like atoms

– Hydrogen is the simplest of all atoms since there is only one electron in it.

– This single electron is expected normally to be present in the lowest energy state n = 1.

– The values of (l) and (m) are both zero and spin quantum numbers can be either +½ or –½.

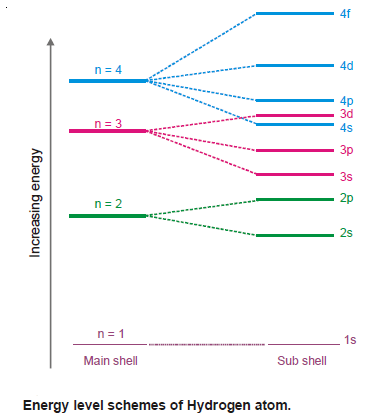
– When this single electron absorbs energy, it may jump to higher energy levels given by (n) or a subshell thereon (represented by l values).

– The spectral study of hydrogen has revealed that its spectral lines correspond to the major energy levels only.

– Thus the energy value of an electron having a particular quantum is fixed, irrespective of the orbital to which it may belong.

– In other words, the energy associated with electrons in s, p, d, and f orbitals of a particular principal quantum number is the same.

– For example, the energy level of 3s, 3p and 3d orbitals is equal

(b) Polyelectron atoms

– Let us first consider a two-electron atom.

– The second electron which may differ from the first electron in spin only, is also accommodated in the 1s orbital, thereby completing the K shell.

– Unlike hydrogen, where there is no such completed shell, the energies of the subsequent electrons coming in various levels and sublevels will be affected.

– Thus it is this completed K shell that affects the energy of the electrons occupying subsequent energy levels.

– For atoms having more than two electrons, the nuclear charge is shielded from the outer electrons by the two K shell electrons.

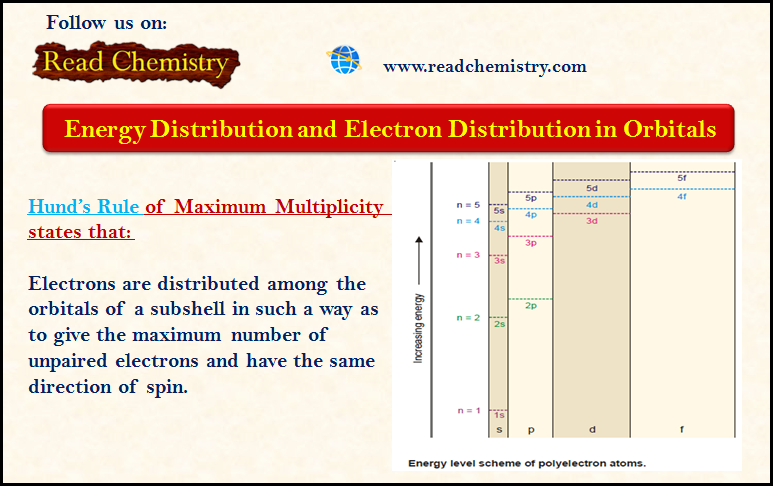
– The effect of the completed K shell of electrons is to make the energy level of any orbital in a principal level (n) dependent upon the value of orbital quantum number (l).

– The dependence of energy of orbitals of a shell on l (l = 0 or s, l = 1 or p etc.) is because of the fact that (s) orbital electrons (l = 0), for example, penetrate near the nucleus and are, therefore, less effectively shielded from the nuclear charge.

– The s electrons (l = 0) being less shielded are drawn inwards and possess lesser energy than p orbital (l = 1) electrons.

– The same argument can be extended for other values of (l).

– Thus within each energy level (n), the various sublevels (different l values orbitals) exhibit slightly different energies.

– The orbitals at a principal level (n) get split up and come to possess different energies, which increase in the same order as the various values of (l).

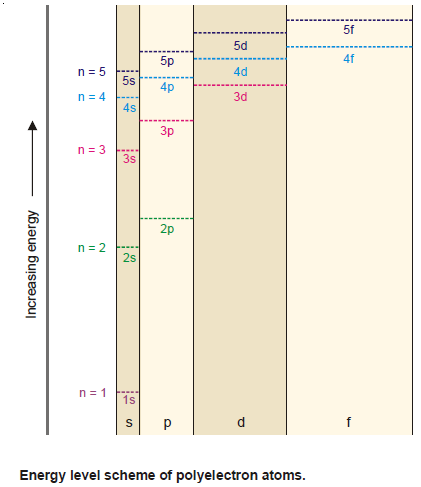
Order of increase of energy values of various orbitals

– Thus for a particular principal level, the energy of the sublevels is in the order:

s < p < d < f

– The energy levels of 3s, 3p, and 3d orbitals are different even though they belong to the same shell n = 3. However, it may be noted that the energy of electrons in the same orbital is the same.

– Thus all 3d orbitals (3d_xy, 3d_yz, 3d_zx, 3dzx, 3d_z2, 3d_x2-y2 ) or 4p orbitals (4p_x, 4p_y, 4p_z) are at the same level of energy, irrespective of their orientation.

– It is also noteworthy from the above diagram that the order of increase of energy values of various orbitals approximately follows the sequence given below:

1s < 2s < 2p < 3s < 3p < 4s < 3d < 4p < 5s < 4d < 5p < 6s < 4f < 5d

– It is, therefore, clear that the 3d orbital electrons belonging to a lower shell (n = 3) possess more energy than 4s orbital electrons which belong to higher shell (n = 4).

– The 3d orbitals lie at a higher energy level than 4s orbital.

Distribution of electrons in orbitals

– In passing along the periodic table of the elements from one element to the other, we find that one electron is added every time to the next atom. Where should the incoming electron go?

– The answer is provided by the possible values of the quantum numbers that can be assigned to the electron in accordance with Pauli’s exclusion principle – prohibiting an orbital to accommodate two electrons with the same set of quantum numbers.

– On the basis of magnetic measurements, which also help to determine the electronic configuration of elements, Hund put forward another empirical rule, popularly known after his name as Hund’s Rule of Maximum Multiplicity.

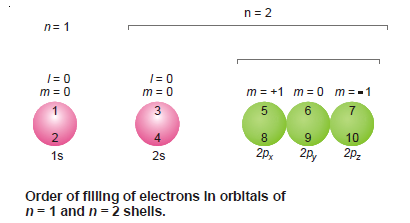
– Thus the orbitals available at a subshell are first filled singly before they begin to pair.

– The following illustration shows the order of filling of electrons in the orbitals of n = 1 and n = 2 shells.

– The orbitals are shown by circles and the order of filling for the first ten electrons is indicated by the numbers entered in them.

– It is also clear from the illustration that no two electrons in an orbital have the same values of all four quantum numbers.

– In fact, three are identical while the fourth quantum number i.e., the spin quantum number is invariably different.

– The electrons in the p orbitals are arranged and accommodated such that they have all obtained one electron first (5th in 2p_x, 6th in 2p_y, 7th in 2p_z) and now they begin to pair up getting the 8th, 9th, and 10th electrons respectively.

Reference: Essentials of Physical Chemistry /Arun Bahl, B.S Bahl and G.D. Tuli / multicolor edition.