Read Chemistry
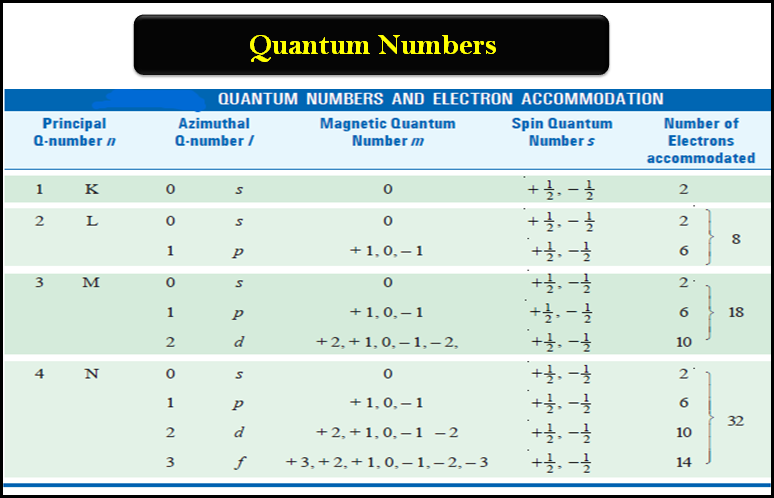
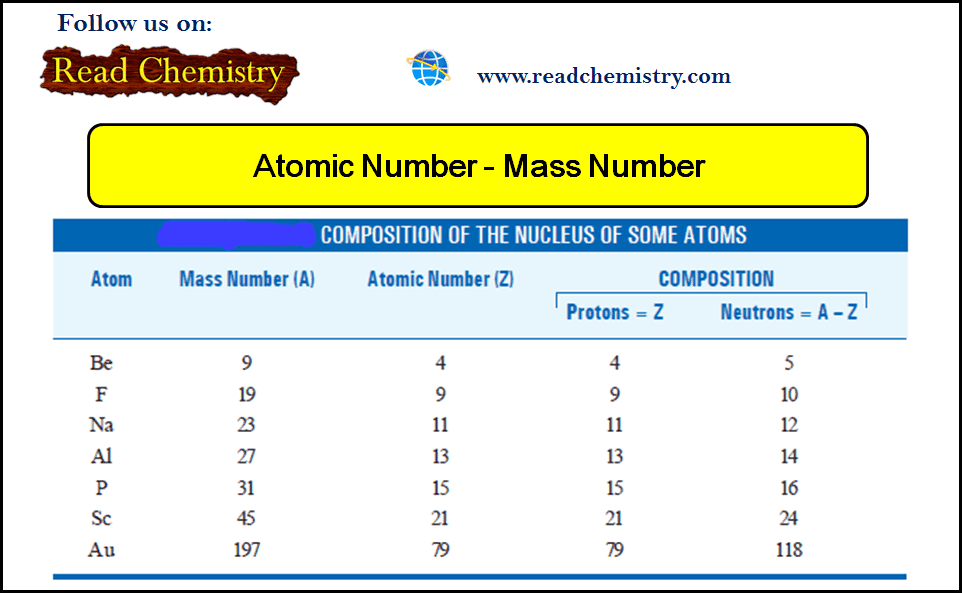
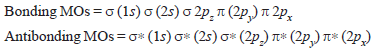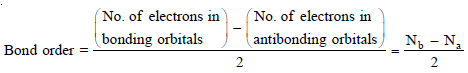Molecular Orbital Theory
– The molecular orbital theory proposed by Hund and Mulliken in 1932 explains the formation of a covalent bond in a better way.
– According to molecular orbital theory all atomic orbitals of the atoms participating in molecule formation get disturbed when the concerned nuclei approach nearer.
– They all get mixed up to give rise to an equivalent number of new orbitals that belong to the molecule now. These are called molecular orbitals.
– Thus every molecule is supposed to have molecular orbitals associated with it in much the same way as a single isolated atom has.
The main features of molecular orbital theory can be summed up as follows:
(1) A molecule is quite different from its constituent atoms.
– All the electrons belong to the constituent atom and are considered to be moving under the influence of all nuclei.
(2) Atomic orbitals of individual atoms combine to form molecular orbitals and these MOs are filled up in the same way as atomic orbitals are formed.
– In other words, Pauli’s exclusion principle, Aufbau principle, and Hund’s rule of maximum multiplicity are followed.
(3) The molecular orbitals have definite energy levels.
(4) The shapes of MOs formed depend upon the shape of combining atomic orbitals.
Linear Combination of Atomic orbitals (LCAO method)
– According to wave mechanics the atomic orbitals can be expressed as wave functions (ψs) which represent the amplitude of electron waves.
– Their values can be calculated from the solutions of Schrödinger’s wave equation.
– In a similar way, Schrödinger’s wave equation can be applied to molecules but with slight difficulty.
– To cope with the difficulty an approximate method known as Linear Combination of atomic orbitals is applied.
– According to this method, the molecular orbitals are formed by the linear combination (addition or subtraction) of atomic orbitals of the constituent atoms of the molecule.
– Let us consider the simplest case of H2 molecule consisting of two hydrogen atoms represented by HA and HB.
– The atomic orbitals of these atoms are represented by the wave functions ψAand ψB.
– When these atoms approach each other there come two possibilities:
(1) Molecular orbital is formed by the addition of wave functions of atomic orbitals. It can be represented by:
– The M.O. formed is called bonding molecular orbital.
– It lowers the energy and brings about the stability in the system.
(2) Molecular orbital is formed by the subtraction of wave functions of atomic orbitals. It can be represented by:
– The MO formed is called antibonding molecular orbital.
– This type of MO corresponds to higher energy state. It has net disruptive effect.
– That is why this MO is termed as antibonding molecular orbital, distinguished by attaching an asterisk (*) mark with the symbolic name of the molecular orbital.
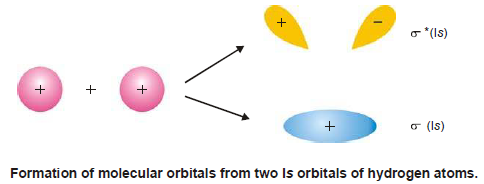
– The molecular orbitals formed by the combination of 1s orbitals of two hydrogen atoms is shown below:
– The wave functions either have (+) or (–) sign.
– The positive sign shown on 1s orbitals of hydrogen atoms shows that these orbitals are spherically symmetrical and their wave functions are associated with +ve sign in all directions.
– In case of p-orbitals one lobe has +ve sign while other has –ve sign.
– The overlapping of atomic orbitals takes place if they have similar signs on their lobes.
– The probability density in bonding and antibonding molecular orbitals is given by the square of the wave functions shown in the equations (1) and (2):
– From equation (3) it is clear that probability density of bonding molecular orbital is greater than the sum of the probability densities of isolated atoms by the factor 2ψA ψB.
– Thus the probability density of electrons in bonding MO is greater than that in either of atomic orbitals (ψA2 or ψB2).
– From equation (4) it is clear that probability density of antibonding MO is lesser than the sum of probability densities of isolated atoms by a factor 2ψA ψB.
– Thus the probability density of electrons in antibonding MO is less than that in either of atomic orbitals (ψA2or ψB2).
– In a similar way, the combination of two 2s orbitals produces a bonding σ (2s) and antibonding σ* (2s) molecular orbitals.
Relative Energies of bonding and antibonding MOs
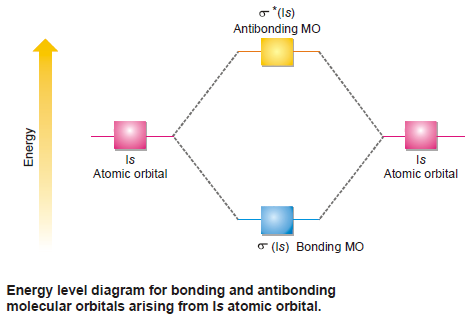
– We have seen above that when atomic orbitals combine, an equivalent number of new orbitals is formed.
– For example, when two 1s orbitals combine two new molecular orbitals are formed.
– One of these pertains to the bonding molecular orbital with lower energy while the other corresponds to higher energy as compared to both the atomic orbitals concerned in the process.
– Thus we find that the number of molecular orbitals formed from atomic orbitals is equal to the number of atomic orbitals responsible for their formation and are of two types as shown below.
Molecular Orbitals from p-Atomic Orbitals
– Combination of p-orbitals is slightly complicated.
– There being three types of 2p orbitals namely 2px, 2py and 2pz directed along the cartesian co-ordinates x, y and z respectively.
– By convention we assume that z-axis is the intermolecular axis.
(1) Combination of 2pz atomic orbitals
– When two 2pz orbitals on two atoms approach each other along the internuclear axis they combine by the addition of electron wave.
– This results in the formation of bonding σ (2pz) orbital while subtraction of electron waves gives rise to antibonding molecular orbital σ* (2pz).
– It is represented as follows :
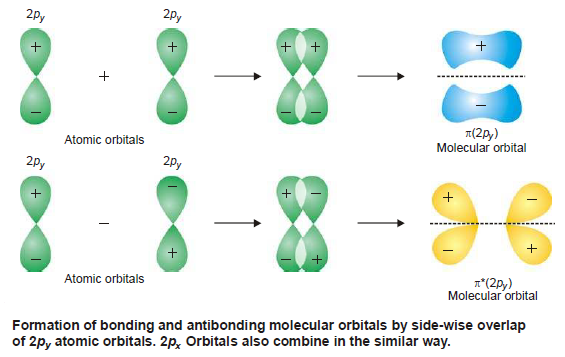
(2) Combination of 2py and 2pxatomic orbitals
– When two 2py or 2px orbitals on two atoms are approaching in a manner that their axes are mutually parallel, they interact to give rise to the formation of molecular orbitals that are not symmetrical about the internuclear axis and are called molecular orbitals represented by π (2py ) or π (2px ) bonding orbitals.
– These π (2py ) and π (2px ) bonding MOs have zero electron density on the plane that contains the nuclear axis (nodal plane), while the electron density is concentrated in two regions above and below the nodal plane.
– The π* (2py ) and π* (2px) antibonding MOs have higher energy than their corresponding molecular and atomic orbitals.
– Since 2py and 2px atomic orbitals on an atom are degenerate (are of equal energy), the π molecular orbitals arising out of them will also be degenerate i.e. π (2py ) and π (2px ) bonding molecular orbitals possess equal energy and the same situation prevails in antibonding molecular orbitals π* (2py ) and π* (2px).
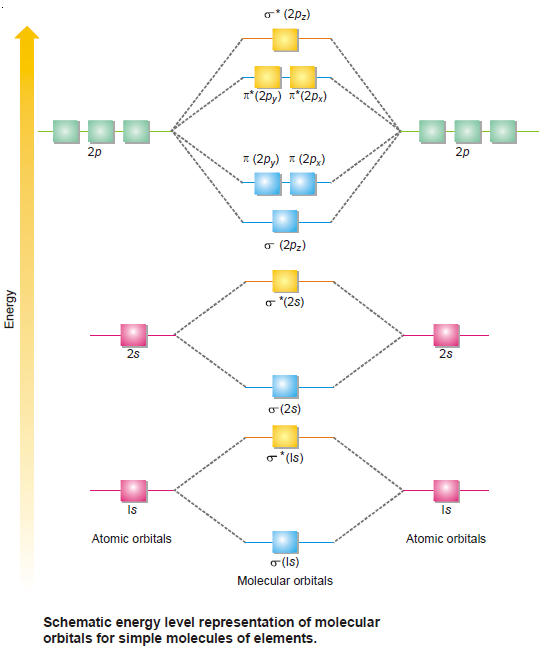
– Since we are concerned here with few simple molecules, the only molecular orbitals which need to be considered are:
– They are arranged in their increasing order of energy as determined by spectroscopic measurements.
– It is clear from Fig (1) that the three 2p atomic orbitals of isolated atoms are all degenerate but this degeneracy splits in the molecular orbitals.
– The σ (2pz) bonding molecular orbital has a lower energy than either of the remaining two degenerate π bonding molecular orbitals –π (2py) and π (2px).
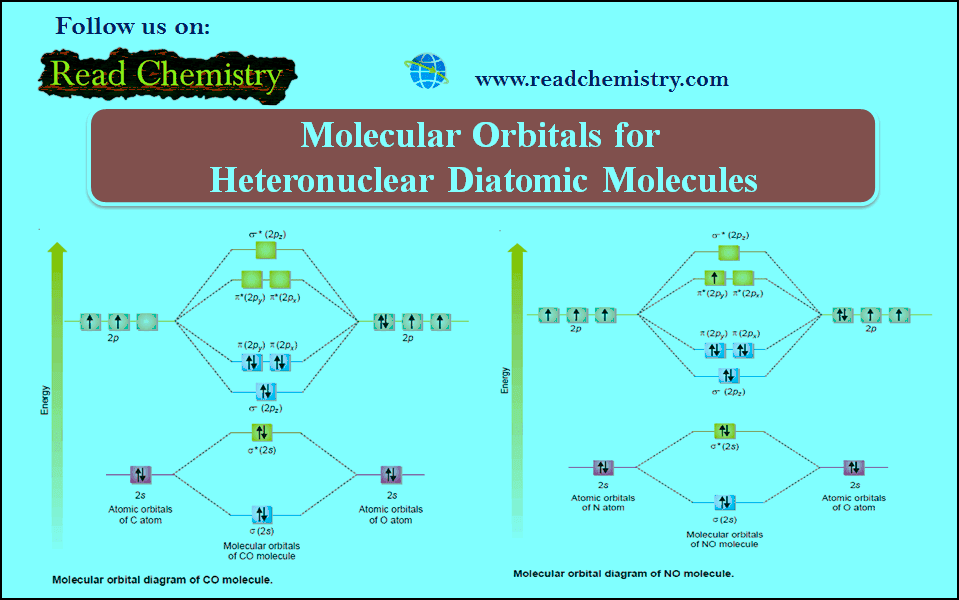
– For diatomic molecules obtained from atom having more than one electronic shell, the inner shells do not appreciably affect the bonding and may be omitted. Such inner electrons are called Non-bonding electrons.
– Electronic structures of simple molecules can be worked out by feeding electrons in the molecular orbitals in the order of increasing energy.
– Here also the Aufbau principle–feeding electrons in the increasing order of energy of orbitals repeats itself.
– This order shown in Fig. (1) may be written as :
(1s) σ∗ (1s) σ (2s) σ∗ (2s) σ (2pz) π (2py) = π (2px) π∗ (2py) = π∗ (2px) σ∗ (2pz)
Conditions for the combination of Atomic Orbitals
– The atomic orbitals may combine when certain conditions are met with.
– For effective combinations of atomic orbitals following are the conditions.
(1) The energies of atomic orbitals should be comparable.
– For homonuclear diatomic molecules of the type X2 similar atomic orbitals combine i.e. 1s orbital of one atom combines with 1s orbital of another and similarly 2s orbital combines with 2s orbital of another atom and so on.
– This means that 1s orbital cannot combine with 2s orbital because of large energy difference between the two orbitals.
– In case homonuclear molecules this condition may not be valid.
(2) The extent of overlap between the atomic orbitals should be to a considerable extent.
– The greater the overlap between the atomic orbitals, the greater is charge density between the nuclei.
(3) The symmetry of the combining atomic orbitals should be the same.
– The atomic orbitals should have the same symmetry about the internuclear axis.
– For example, 2s orbital of one atom can combine with 2s or 2pz orbital of another atom but not with the 2py or 2pxorbital.
– In other words ++ or – – interaction is allowed. It is made clear in the following diagram:
Allowed Combinations of Atomic orbitals
– Due to symmetry reasons allowed combinations of atomic orbitals are given in the following table:
Energy Levels of Molecular orbitals
– We have already discussed that the energy of a bonding MO is lesser than that of atomic orbital whereas the energy of an antibonding MO is higher than the atomic orbitals from which it has been formed.
– The total energy of a diatomic molecule can also be plotted against the internuclear distance between its atoms.
– When these two atoms are brought closer the energy changes are shown in the following figure:
– The curve (P) represents the formation of a bonding molecular orbital and the curve (Q) represents the formation of an antibonding molecular orbital.
– It is clear from the curve (Q) that repulsive forces dominate during the formation of an antibonding molecular orbital.
– During the formation of a bonding molecular orbital the energy starts decreasing and reaches to a minimum value which corresponds to the bond length between the two atoms (r0).
– At a distance less than r0 the repulsive forces start dominating over the attractive forces and energy starts increasing.
Difference Between Bonding and Antibonding Molecular Orbitals
– The difference between bonding and antibonding orbitals is summarised below:
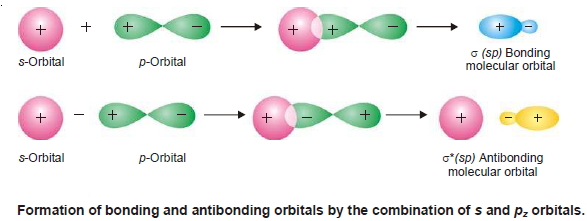
Combination of s and pz-orbitals
– s and pz-orbitals can also combine in a similar way along internuclear axis to form bonding and antibonding molecular orbitals as shown in the following figure:
Difference between Sigma and Pi molecular orbitals
– The main points of difference between sigma and Pi molecular orbitals can be summed up in the following table:
Bond Order
– How many are the bonds in a molecule or Bond order is correctly predicted by the Molecular Orbital theory.
– The number of bonds in a molecule is one-half of the difference of the number of electrons in the bonding molecular orbitals and the number of electrons in the antibonding molecular orbitals. Mathematically,
– In common practice, only MOs formed from valence orbitals are considered for determining bond order.
– The predicted bond orders are found to be in conformity with other methods of determining it.
– Thus Molecular Orbital theory helps in establishing whether the existence of a bond is feasible or not.
– For instance, the formation of He2 molecule, discussed in the following section, is completely ruled out as the bond order predicted is zero.
– In general,
(a) A molecule is stable if Nb > Na
(b) A molecule is unstable if Nb < Na
Information given by Bond order
– The bond order as determined by the above formula is very helpful as it gives us the following valuable information :
(1) Stability of the Molecule/Ion
– A molecule/ion is stable if Nb > Na
(2) Bond Dissociation Energy
– It depends upon the bond order.
– Greater the bond order greater is the bond dissociation energy.
(3) Bond Length
– Bond order is inversely proportional to the bond length.
– Higher the bond order, smaller the bond length.
(4) Magnetic Properties
– The presence of unpaired electrons in Molecular orbitals of a species makes it paramagnetic in nature.
– The greater the number of unpaired electrons, the more will be its paramagnetic character.
– On the other hand, if there are no unpaired electrons in MOs the species will be diamagnetic in nature.
Reference: Essentials of Physical Chemistry /Arun Bahl, B.S Bahl and G.D. Tuli / multicolour edition.
