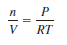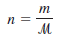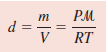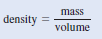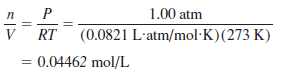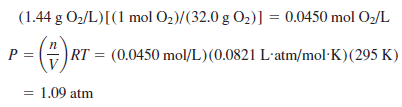Density of gas: Definition, Equation, Solved Examples

– In this subject, we will discuss the Density of gas (Definition, Equation, Solved Examples)

The Density of gas

– From the ideal gas equation:

– If we rearrange the ideal gas equation, we can calculate the density of a gas:

– The number of moles of the gas, n, is given by:

– where m is the mass of the gas in grams and µ is its molar mass. Therefore

– Because density, d, is mass per unit volume, we can write:

– Unlike molecules in condensed matter (that is, in liquids and solids), gaseous molecules are separated by distances that are large compared with their size.

– Consequently, the density of gases is very low under atmospheric conditions.

– For this reason, gas densities are usually expressed in grams per liter (g/L) rather than grams per milliliter (g/mL).

Solved problems on the Density of gas

Problem (1) 

Calculate the density of carbon dioxide (CO₂) in grams per liter (g/L) at 0.990 atm and 55^oC.

Strategy:

– We need the combined gas Equation to calculate gas density.

– Is sufficient information provided in the problem? What temperature unit should be used?

Solution:

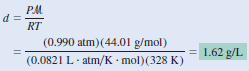
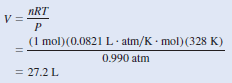
– To use the combined gas Equation, we convert temperature to kelvins ( T = 273 + 55 = 328 K) and use 44.01 g for the molar mass of CO₂:

– Alternatively, we can solve for the density by writing:

– Assuming that we have 1 mole of CO₂, the mass is 44.01 g.

– The volume of the gas can be obtained from the ideal gas equation

– Therefore, the density of CO₂ is given by:

Comment:

– ln units of grams per milliliter, the gas density is 1.62 × 10^-3 g/mL, which is a very small number.

– In comparison, the density of water is 1.0 g/mL and that of gold is 19.3 g/cm³.

Problem (2)

Determine the density of nitrogen at STP.

Solution:

– It is easy to calculate the number of moles of nitrogen gas per liter using the ideal gas law:

– The density, the number of grams per liter, is obtained using the molar mass as a conversion factor:

Problem (3)

Calculate the pressure at at 22 ^oC which oxygen has a density of 1.44 g/L.

Solution:

– We first change the density in grams per liter to moles per liter, then use that value in the ideal gas law: