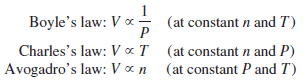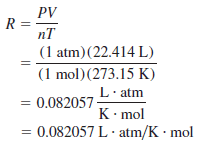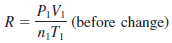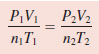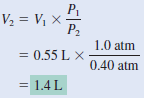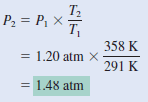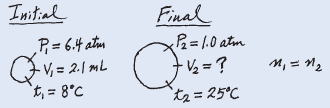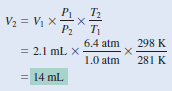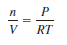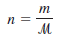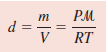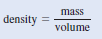Ideal Gas Equation: Definition, Formula, Notes
– In this subject, we will discuss the Ideal Gas Equation (Definition, Formula, Notes)
The Ideal Gas Equation
– Let us summarize the gas laws we have discussed so far:
– We can combine all three expressions to form a single master equation for the behavior of gases:
– This Equation is called the ideal gas equation where R, the proportionality constant, is called the gas constant.
– The ideal gas equation, describes the relationship among the four variables P, V, T, and n.
Important Notes of Ideal Gas
(1) An ideal gas is a hypothetical gas whose pressure-volume-temperature behavior can be completely accounted for by the ideal gas equation.
(2) The molecules of an ideal gas do not attract or repel one another, and their volume is negligible compared with the volume of the container.
(3) Although there is no such thing in nature as an ideal gas, the ideal gas approximation works rather well for most reasonable temperature and pressure ranges.
(4) we can safely use the ideal gas equation to solve many gas problems.
The gas constant
– Before we can apply the ideal gas equation to a real system, we must evaluate the gas constant R.
– At 0oC (273.15 K) and 1 atm pressure, many real gases behave like an ideal gas.
– Experiments show that under these conditions, 1 mole of an ideal gas occupies 22.414 L, which is somewhat greater than the volume of a basketball, as shown in The following Figure:
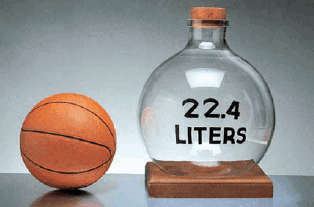
– The conditions 0oC and 1 atm are called standard temperature and pressure, often abbreviated STP.
– From the ideal gas Equation, we can write:
– The dots between L and atm and between K and mol remind us that both L and atm are in the numerator and both K and mol are in the denominator.
– For most calculations, we will round off the value of R to three significant figures (0.0821 L.atm/K.mol) and use 22.41 L for the molar volume of a gas at STP.
– Example (1) shows that if we know the quantity, volume, and temperature of a gas, we can calculate its pressure using the ideal gas equation.
– Unless otherwise stated, we assume that the temperatures given in °C in calculations are exact so that they do not affect the number of significant figures.
Solved problem on Ideal Gas Equation
Problem (1)
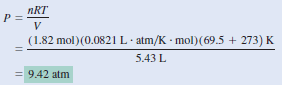
Sulfur hexafluoride (SF6) is a colorless, odorless, very unreactive gas. Calculate the pressure (in atm) exerted by 1.82 moles of the gas in a steel vessel of volume 5.43 L at 69.5oC.
Strategy:
– The problem gives the amount of the gas and its volume and temperature.
– Is the gas undergoing a change in any of its properties?
– What equation should we use to solve for the pressure?
– What temperature unit should we use?
Solution:
– Because no changes in gas properties occur, we can use the ideal gas equation to calculate the pressure.
– Rearranging the ideal gas Equation, we write:
– By using the fact that the molar volume of a gas occupies 22.41 L at STP, we can calculate the volume of a gas at STP without using the ideal gas equation.
Problem (2)
Calculate the volume (in liters) occupied by 7.40 g of NH3 at STP?
Strategy:
– What is the volume of one mole of an ideal gas at STP?
– How many moles are there in 7.40 g of NH3?
Solution:
– Recognizing that 1 mole of an ideal gas occupies 22.41 L at STP and using the molar mass of NH3 (17.03 g), we write the sequence of conversions as
so the volume of NH3 is given by:
– It is often true in chemistry, particularly in gas-law calculations, that a problem can be solved in more than one way.
– Here the problem can also be solved by first converting 7.40 g of NH3to number of moles of NH3 , and then applying the ideal gas equation ( V = nRT/P ). Try it.
Check:
– Because 7.40 g of NH3 is smaller than its molar mass, its volume at STP should be smaller than 22.41 L.
– Therefore, the answer is reasonable.
Combined gas law Equation
– The ideal gas equation is useful for problems that do not involve changes in P , V , T , and n for a gas sample.
– Thus, if we know any three of the variables we can calculate the fourth one using the equation.
– At times, however, we need to deal with changes in pressure, volume, and temperature, or even in the amount of gas.
– When conditions change, we must employ a modified form of the ideal gas equation that takes into account the initial and final conditions.
– We derive the modified equation as follows.
– From the Ideal gas equation:
– It is interesting to note that all the gas laws can be derived from the previous Equation.
– If n1 = n2, as is usually the case because the amount of gas normally does not change, the equation then becomes:
Solved Problems On Combined gas law Equation
Problem (1)
An inflated helium balloon with a volume of 0.55 L at sea level (1.0 atm) is allowed to rise to a height of 6.5 km, where the pressure is about 0.40 atm. Assuming that the temperature remains constant, what is the final volume of the balloon?
Strategy:
– The amount of gas inside the balloon and its temperature remain constant, but both the pressure and the volume change.
– What gas law do you need?
solution:
– We start with Equation:
– Because n1= n2 and T1 = T2 ,
– which is Boyle’s law.
– The given information is tabulated:
Check:
– When the pressure applied on the balloon is reduced (at constant temperature), the helium gas expands and the balloon’s volume increases.
– The final volume is greater than the initial volume, so the answer is reasonable.
Problem (2)
Argon is an inert gas used in light bulbs to retard the vaporization of the tungsten filament. A certain light bulb containing argon at 1.20 atm and 18oC is heated to 85oC at constant volume. Calculate its final pressure (in atm).
Strategy:
– The temperature and pressure of argon change but the amount and volume of gas remain the same.
– What equation would you use to solve for the final pressure?
– What temperature unit should you use?
Solution:
– from combined gas law:
– Because n1 = n2 and V1= V2 , the Equation becomes:
– which is Charles’s law.
– Next, we write
Check:
– At constant volume, the pressure of a given amount of gas is directly proportional to its absolute temperature.
– Therefore the increase in pressure is reasonable.
Problem (3)
A small bubble rises from the bottom of a lake, where the temperature and pressure are 8oC and 6.4 atm, to the water’s surface, where the temperature is 25oC and the pressure is 1.0 atm. Calculate the final volume (in mL) of the bubble if its initial volume was 2.1 mL.
Strategy:
– In solving this kind of problem, where a lot of information is given, it is sometimes helpful to make a sketch of the situation, as shown here:
– What temperature unit should be used in the calculation?
Solution:
– According to the combined gas law Equation:
– We assume that the amount of air in the bubble remains constant, that is, n1 = n2so that
– The given information is summarized:
Check:
– We see that the final volume involves multiplying the initial volume by a ratio of pressures (P1/P2) and a ratio of temperatures (T2/T1). Recall that volume is inversely proportional to pressure, and volume is directly proportional to temperature.
– Because the pressure decreases and temperature increases as the bubble rises, we expect the bubble’s volume to increase.
– In fact, here the change in pressure plays a greater role in the volume change.
Density of gas
– If we rearrange the ideal gas equation, we can calculate the density of a gas:
– where m is the mass of the gas in grams and µ is its molar mass. Therefore
– Because density, d, is mass per unit volume, we can write:
– Unlike molecules in condensed matter (that is, in liquids and solids), gaseous molecules are separated by distances that are large compared with their size.
– Consequently, the density of gases is very low under atmospheric conditions.
– For this reason, gas densities are usually expressed in grams per liter (g/L) rather than grams per milliliter (g/mL).
Solved problems on the Density of gas
Problem (1)
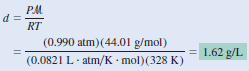
Calculate the density of carbon dioxide (CO2 ) in grams per liter (g/L) at 0.990 atm and 55oC.
Strategy:
– We need the combined gas Equation to calculate gas density.
– Is sufficient information provided in the problem?
– What temperature unit should be used?
Solution:
– To use the combined gas Equation, we convert temperature to kelvins ( T = 273 + 55 = 328 K) and use 44.01 g for the molar mass of CO2 :
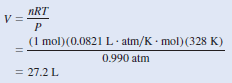
– Alternatively, we can solve for the density by writing:
– Assuming that we have 1 mole of CO2, the mass is 44.01 g.
– The volume of the gas can be obtained from the ideal gas equation
– Therefore, the density of CO2 is given by:
Comment:
– ln units of grams per milliliter, the gas density is 1.62 × 10-3 g/mL, which is a very small number.
– In comparison, the density of water is 1.0 g/mL and that of gold is 19.3 g/cm3.
- Reference: Chemistry / Raymond Chang, Williams College /(10th edition).