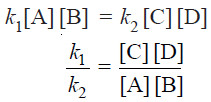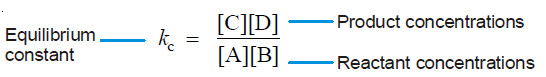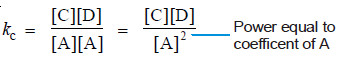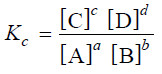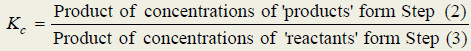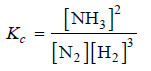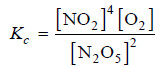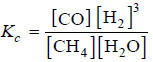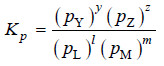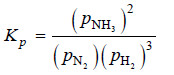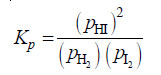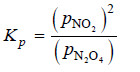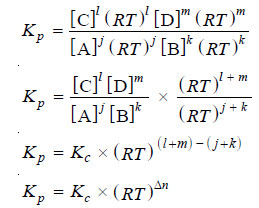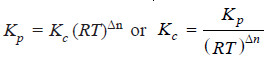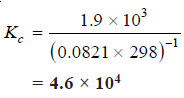Equilibrium Constant Expression

Equilibrium constant: Equilibrium law

– Now we will find the Expression of Equilibrium Constant.

– Let us consider a general reaction

A + B ↔ C + D

– and let [A], [B], [C] and [D] represent the molar concentrations of A, B, C and D at the equilibrium point.

– According to the Law of Mass action.

Rate of forward reaction ∝ [A] [B] = k₁ [A] [B]

Rate of reverse reaction ∝ [C][D] = k₂ [C][D]

– where k₁ and k₂ are rate constants for the forward and reverse reactions.

– At equilibrium, rate of forward reaction = rate of reverse reaction.

Therefore,

– At any specific temperature k₁/k₂ is constant since both k₁ and k₂ are constants.

– The ratio k₁/k₂ is called Equilibrium constant and is represented by the symbol K_c , or simply k.

– The subscript (c) indicates that the value is in terms of concentrations of reactants and products.

– The equation (1) may be written as :

– This equation is known as the Equilibrium constant expression or Equilibrium law

– Consider the reaction:

– Here, the forward reaction is dependent on the collisions of each of two A molecules.

– Therefore, for writing the equilibrium expression, each molecule is regarded as a separate entity i.e.,

A + A ↔ C + D

Then the equilibrium constant expression is:

As a general rule, if there are two or more molecules of the same substance in the chemical equation, its concentration is raised to the power equal to the numerical coefficient of the substance in the equation.

Equilibrium Constant Expression for a Reaction in General Terms

– The general reaction may be written as:

aA + bB ↔ cC + dD

– where a, b, c and d are numerical quotients of the substance, A, B, C and D respectively.

– The equilibrium constant expression is:

– where K_c is the Equilibrium constant.

– The general definition of the equilibrium constant may thus be stated as : the product of the equilibrium concentrations of the products divided by the product of the equilibrium concentrations of the reactants, with each concentration term raised to a power equal to the coefficient of the substance in the balanced equation

How to Write the Equilibrium Constant Expression?

(1) Write the balanced chemical equation for the equilibrium reaction. By convention, the substances on the left of the equation are called the reactants and those on the right, the products.

(2) Write the product of concentrations of the (products) and raise the concentrations of each substance to the power of its numerical quotient in the balanced equation.

(3) Write the product of concentrations of (reactants) and raise the concentration of each substance to the power of its numerical quotient in the balanced equation.

(4) Write the equilibrium expression by placing the product concentrations in the numerator and reactant concentrations in the denominator. That is,

Solved problems on equilibrium constant expression

Solved problem(1): Give the equilibrium constant expression for the reaction

N_2(g) + 3H2 (g) ↔ 2NH3(g)

Solution:

(1) The equation is already balanced. The numerical quotient of H₂ is 3 and of NH₃ is 2.

(2) The concentration of the ‘product’ NH₃ is [NH₃]²

(3) The product of concnentrations of the reactants is [N₂] [H₂]³

(4) Therefore, the equilibrium constant expression is:

Solved problem(2): Write the equilibrium constant expression for the reaction

N₂O_5(g) ↔ NO_2(g) + O_{2 (g)}

Solution:

(1) The equation as written is not balanced. Balancing yields

2N₂O_5(g) ↔ 4NO_2(g) + O_{2 (g)}

(2) The quotient of the product NO₂ is 4 and of the reactant N₂O₅ it is 2.

(3) The product of the concentrations of products is [NO₂]⁴ [O₂]

(4) The concentration of the reactant is [N₂O₅]²

(5) The equilibrium constant expression can be written as:

Solved problem(3): What is the equilibrium constant expression of the reaction

CH_{4 (g)} + H2O_(g) ↔ CO_(g) + 3H_2(g)

Solution:

– Write the product of concentrations of ‘products’ divided by the product of concentrations of ‘reactants’.

– The concentration of H₂ is to be raised by its quotient in the equation. Thus, theequilibrium constant expression is:

Equilibrium Constant Expression in Terms of Partial Pressures

– When all the reactants and products are gases, we can also formulate the equilibrium constant expression in terms of partial pressure.

– The relationship between the partial pressure (p) of any one gas in the equilibrium mixture and the molar concentration follows from the general ideal gas equation:

pV = nRT  or  P = (n/V)RT

– The quantity (n/V) is the number of moles of the gas per unit volume and is simply the molar concentration. Thus,

p = (Molar concentration) × RT

– i.e., the partial pressure of a gas in the equilibrium mixture is directly proportional to its molar concentration at a given temperature.

– Therefore, we can write the equilibrium constant expression in terms of partial pressure instead of molar concentrations.

– For a general reaction

l L_(g) + mM_(g) ↔ yY_(g) + zZ_(g)

– the equilibrium law or the equilibrium constant may be written as:

– Here K_p is the equilibrium constant, the subscript (p) referring to partial pressure. Partial pressures are expressed in atmospheres.

Solved problem

Solved problem(1): Write the equilibrium constant expression for the synthesis of ammonia,

N_2(g) + 3H_2(g) ↔ 2NH_3(g)

Solution:

Solved problem(2): Using partial pressures, write the equilibrium law for the reaction:

H2(g) + I2(g) ↔ 2HI(g)

Solution:

Solved problem(3): What is the expression Kp for the reaction

N2O4 (g) ↔ 2NO2(g)

Solution:

– For K_p we use the partial pressure in the equilibrium constant expression. Therefore,

How K_c and K_p are ralated?

– Let us consider a general reaction

jA + kB ↔ lC + mD

where all reactants and products are gases. We can write the equilibrium constant expression in terms of partial pressures as:

(1)

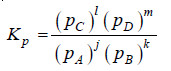
– Assuming that all these gases constituting the equilibrium mixture obey the ideal gas equation, the partial pressure (p) of a gas is:

where (n/V) is the molar concentration. Thus the partial pressures of individual gases, A, B, C and D are:

P_A = [A] RT ; p_B = [B] RT ; p_C = [C] RT ; p_D = [D] RT

Substituting these values in equation (1), we have:

where Δn = (l + m) – (j + k), the difference in the sums of the coefficients for the gaseous products and reactants.

From the expression (2) it is clear that when Δn = 0, K_p = K_c.

Solved problem

Solved problem(1): At 500°C, the reaction between N₂ and H₂ to form ammonia has K_c = 6.0 × 10^–2. What is the numerical value of K_p for the reaction?

Solution:

Here, we will use the general expression

K_p = K_c (RT)^Δn

For the reaction:

N₂ + 3H₂ ↔ 2NH₃

Δn = (sum of quotients of products) – (sum of quotients of reactants)
= 2 – 4 = – 2
Kc = 6.0 × 10^–2
T = 500 + 273 = 773 K
R = 0.0821
Substituting the value of R, T, K_c and Δn in the general expression, we have
Kp = (6.0 × 10^–2) [(0.0821) × (773)]^–2
= 1.5 × 10^–5

Solved problem(2): The value of K_p at 25°C for the reaction:

2NO_(g) + Cl_{2 (g)} ↔ 2NOCl_(g)

is 1.9 × 10³ atm^–1. Calculate the value of K_c at the same temperature.

Solution:

We can write the general expression as:

T = 25 + 273 = 298 K
R = 0.0821
Δn = 2 – ( 2 + 1) = – 1
Kp = 1.9 × 10³

Substituting these values in the general expression: