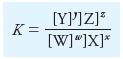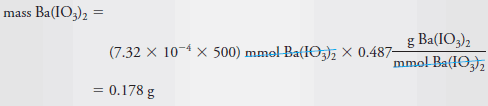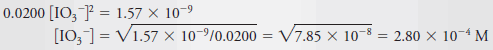Solubility Product Ksp: Definition, Formula, Problems
– In this subject, we will discuss the Solubility Product (Ksp): Definition, Formula, Problems

Solubility Product Constant Ksp
– Most, but not all, sparingly soluble salts are essentially completely dissociated in a saturated aqueous solution.
– For example, when an excess of barium iodate is equilibrated with water, the dissociation process is adequately described by the equation:
Using Equation:
we write:
– The denominator represents the molar concentration of Ba(IO3)2in the solid, which is a phase that is separate from but in contact with the saturated solution.
– The concentration of a compound in its solid state is, however, constant.
– In other words, the number of moles of Ba(IO3)2 divided by the volume of the solid Ba(IO3)2 is constant no matter how much excess solid is present.
– Therefore, the previous equation can be rewritten in the form:
– where the new constant is called the solubility product constant or the solubility product.
– It is important to appreciate that the Equation above shows that the position of this equilibrium is independent of the amount of Ba(IO3)2 as long as some solid is present.
– In other words, it does not matter whether the amount is a few milligrams or several grams.
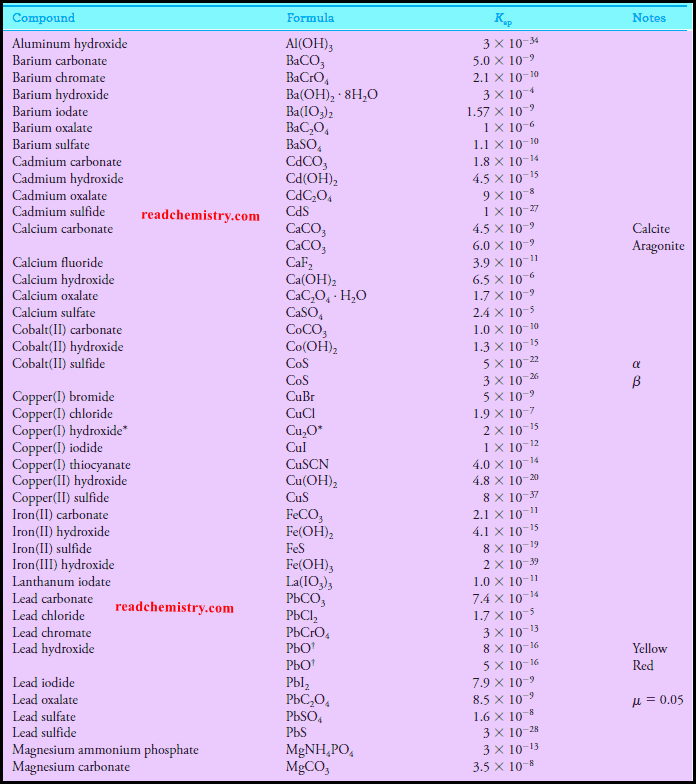
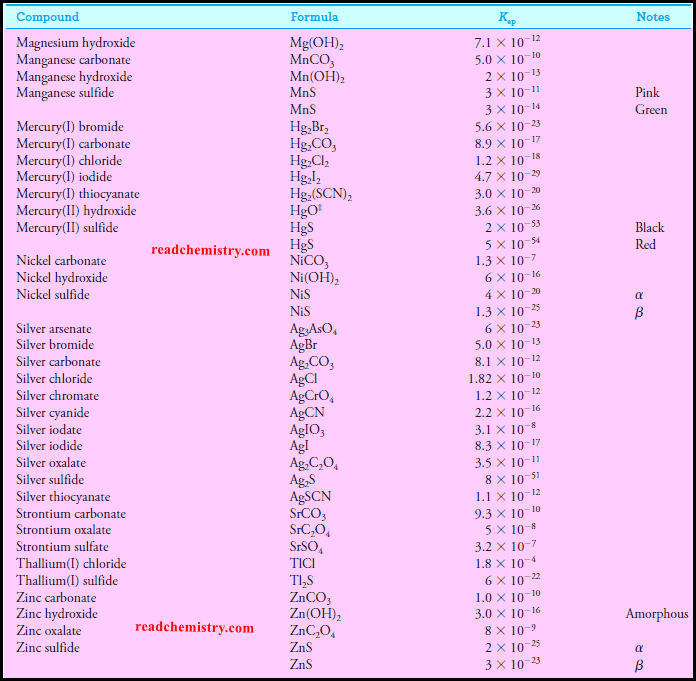
Solubility product constant at 25 °C inorganic salts
– The examples that follow demonstrate some typical uses of solubility product expressions.
The Solubility of a Precipitate in Pure Water
With the solubility product expression, we can calculate the solubility of a sparingly soluble substance that ionizes completely in water.
Example (1):
What mass (in grams) of Ba(IO3)2 (487 g/mol) can be dissolved in 500 mL of water at 25 °C?
Solution:
– The solubility product constant for Ba(IO3)2 is 1.57 × 10-9 (see table above).
– The equilibrium between the solid and its ions in solution is described by the equation:
– The equation describing the equilibrium reveals that 1 mol of Ba2+ is formed for each mole of Ba(IO3)2 that dissolves. Therefore,
– Since two moles of iodate are produced for each mole of barium ion, the iodate concentration is twice the barium ion concentration:
– Substituting this last equation into the equilibrium-constant expression gives:
– Since 1 mol Ba2+ is produced for every mole of Ba(IO3)2,
– To compute the number of millimoles of Ba(IO3)2 dissolved in 500 mL of solution, we write
– The mass of Ba(IO3)2 in 500 mL is given by:
The Effect of a Common Ion on the Solubility of a Precipitate
– The common-ion effect is a mass-action effect predicted by Le Châtelier’s principle and is demonstrated by the following examples.
Example (2) on Solubility Product Ksp
Calculate the molar solubility of Ba(IO3)2 in a solution that is 0.0200 M in Ba(NO3)2.
Solution
– The solubility is not equal to [Ba2+] in this case because Ba(NO3) 2 is also a source of barium ions.
– We know, however, that the solubility is related to [IO3–]:
– There are two sources of barium ions: Ba(NO3)2 and Ba(IO3)2.
– The contribution from the nitrate is 0.0200 M, and that from the iodate is equal to the molar solubility, or ½ [IO3–]. Thus,
– By substituting these quantities into the solubility product expression, we find that
– Since this is a cubic equation, we would like to make an assumption that would simplify the algebra required to find [IO3–].
– The small numerical value of Ksp suggests that the solubility of Ba(IO3)2 is quite small, and this finding is confirmed by the result obtained in Example (1).
– Also, barium ion from Ba(NO3)2 will further suppress the limited solubility of Ba(IO3)2.
– Therefore, it seems reasonable to assume that 0.0200 is large with respect to ½ [IO3–] to find a provisional answer to the problem.
– That is, we assume that ½ [IO3–] << 0.0200, so
– The original equation then simplifies to:
– The assumption that (0.0200 + ½ × 2.80 × 10-4) ~ 0.0200 causes a minimal error because the second term, representing the amount of Ba2+arising from the dissociation of Ba(IO3)2, is only about 0.7% of 0.0200.
– Usually, we consider an assumption of this type to be satisfactory if the discrepancy is less than 10%. Finally, then,
– If we compare this result with the solubility of barium iodate in pure water (Example 1), we see that the presence of a small concentration of the common ion has decreased the molar solubility of Ba(IO3)2 by a factor of about 5.
Example (3) on Solubility Product Ksp
Calculate the solubility of Ba(IO3)2 in a solution prepared by mixing 200 mL of 0.0100 M Ba(IO3)2 with 100 mL of 0.100 M NaIO3.
Solution
– First, establish whether either reactant is present in excess at equilibrium.
– The amounts taken are:
– If the formation of Ba(IO3)2 is complete:

– Thus,

– As in Example (1),

– In this case, however,
– where 2[Ba2+] represents the iodate contributed by the sparingly soluble Ba(IO3)2.
– We find a provisional answer after assuming that [IO3–] ~ 0.0200. Therefore,
– Since the provisional answer is nearly four orders of magnitude less than 0.0200 M, our approximation is justified, and the solution does not need further refinement.
– Notice that the results from the last two examples demonstrate that an excess of iodate ions is more effective in decreasing the solubility of Ba(IO3)2 than the same excess of barium ions.
Reference: Fundamentals of analytical chemistry / Douglas A. Skoog, Donald M. West, F. James Holler, Stanley R. Crouch. (ninth edition), 2014. USA