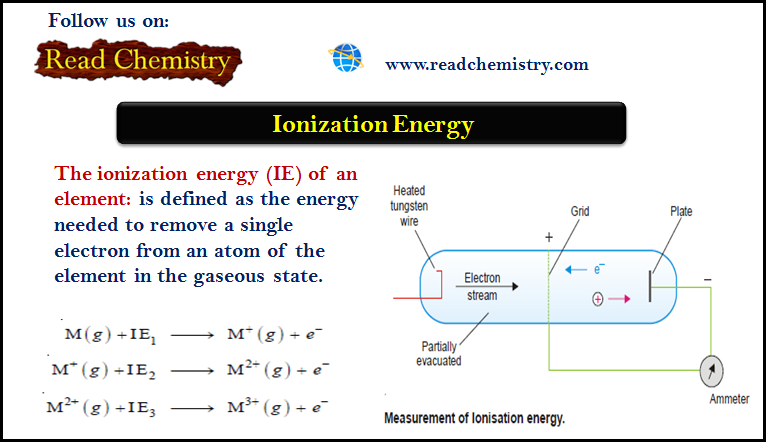
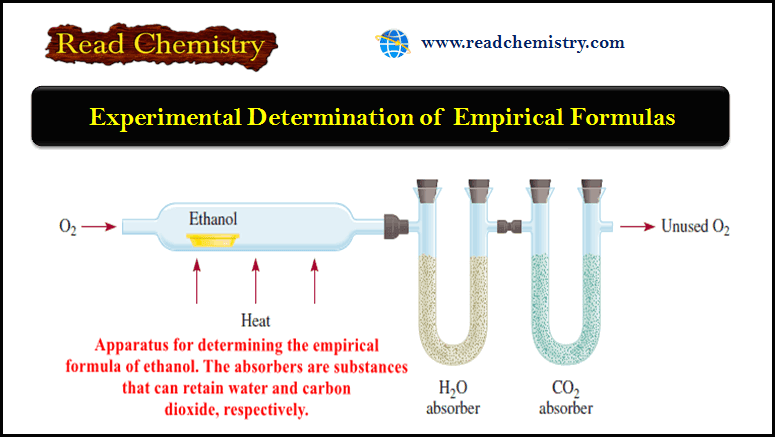
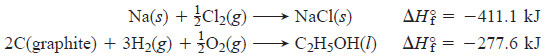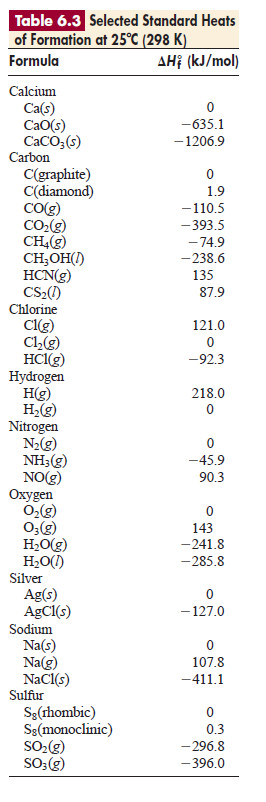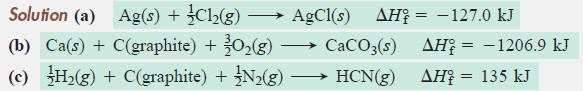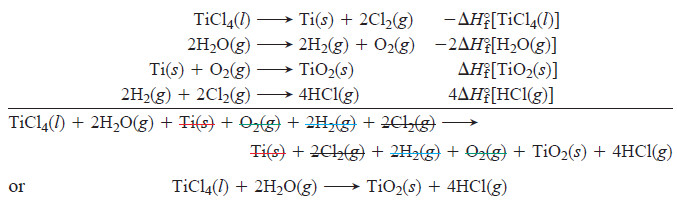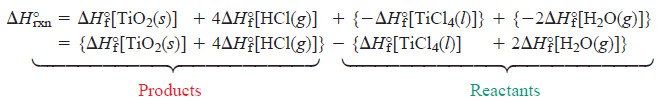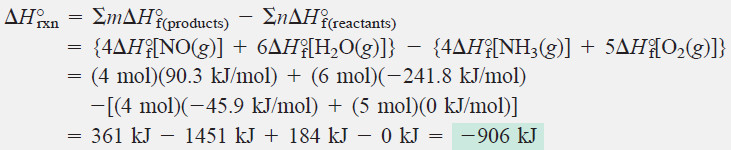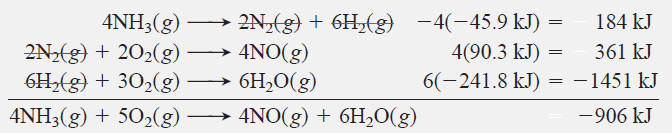Standard Heats of Reaction (ΔH°rxn)
In this subject, we talk about Standard Heats of Reaction (ΔH°rxn)
Standard Heats of Reaction (ΔH°rxn)
– In this subject, we see how Hess’s law is used to determine the ΔH values of an enormous number of reactions.
– To begin we must take into account that thermodynamic variables, such as ΔH, vary somewhat with conditions.
– Therefore, to use heats of reaction, as well as other thermodynamic data that we will encounter in later topics, chemists have established standard states, a set of specified conditions and concentrations:
(1) For a gas, the standard state is 1 atm* with the gas behaving ideally.
(2) For a substance in aqueous solution, the standard state is 1 M concentration.
(3) For a pure substance (element or compound), the standard state is usually the most stable form of the substance at 1 atm and the temperature of interest.
– In this text, that temperature is usually 25°C (298 K).
– We use the standard-state symbol (shown here as a degree sign) to indicate these standard states.
– In other words, when the heat of reaction, ΔH°rxn, has been measured with all the reactants and products in their standard states, it is referred to as the standard heat of reaction, ΔH°rxn.
Formation Equations and Their Standard Enthalpy Changes
– In a formation equation, 1 mole of a compound forms from its elements.
– The standard heat of formation (ΔH°f ) is the enthalpy change for the formation equation when all the substances are in their standard states.
– For instance, the formation equation for methane (CH4) is:
– Thus, the standard heat of formation of methane is -74.9 kJ/mol.
– Some other examples are
Standard heats of formation have been tabulated for many substances.
– The dollowing table shows ΔH°f values for several
– The values in the preivious Table were selected to make two points:
1. An element in its standard state is assigned a ΔH°f of zero.
– For example, note that ΔH°f 0 for Na(s), but ΔH°f = 107.8 kJ/mol for Na(g).
– These values mean that the gaseous state is not the most stable state of sodium at 1 atm and 298.15 K, and that heat is required to form Na(g).
– Note also that the standard state of chlorine is Cl2 molecules, not Cl atoms.
– Several elements exist in different forms, only one of which is the standard state.
– Thus, the standard state of carbon is graphite, not diamond, so ΔH°f of C(graphite) = 0.
– Similarly, the standard state of oxygen is dioxygen (O2), not ozone (O3), and the standard state of sulfur is S8 in its rhombic crystal form, rather than its monoclinic form.
2. Most compounds have a negative ΔH°f .
– That is, most compounds have exothermic formation reactions under standard conditions: heat is given off when the compound forms.
Solved Problem
Write balanced equations for the formation of 1 mole of each of the following compounds from their elements in their standard states, and include ΔH°f .
(a) Silver chloride, AgCl, a solid at standard conditions
(b) Calcium carbonate, CaCO3, a solid at standard conditions
(c) Hydrogen cyanide, HCN, a gas at standard conditions
Solution:
Plan:
– We write the elements as the reactants and 1 mol of the compound as the product, being sure all substances are in their standard states.
– Then, we balance the atoms and obtain the ΔH°f values from preivious Table.
Determining ΔH°rxn from ΔH°f Values of Reactants and Products
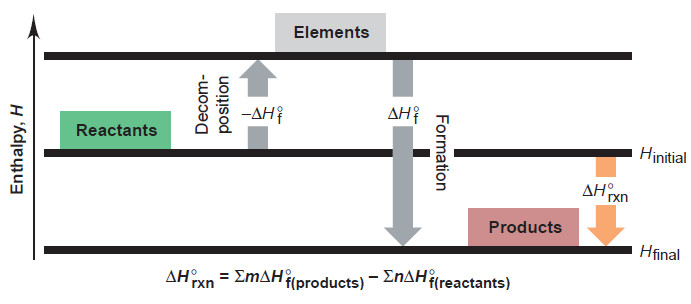
– By applying Hess’s law, we can use ΔH°f values to determine ΔH°rxn for any reaction.
– All we have to do is view the reaction as an imaginary two-step process.
Step 1. Each reactant decomposes to its elements. This is the reverse of the formation reaction for each reactant, so each standard enthalpy change is ΔH°f .
Step 2. Each product forms from its elements. This step is the formation reaction for each product, so each standard enthalpy change is ΔH°f .
– According to Hess’s law, we add the enthalpy changes for these steps to obtain the overall enthalpy change for the reaction (ΔH°rxn).
– The following Figure depicts the conceptual process.
– Suppose we want ΔH°rxn for
– We write this equation as though it were the sum of four individual equations, one for each compound.
– The first two of these equations show the decomposition of the reactants to their elements (reverse of their formation), and the second two show the formation of the products from their elements:
– It’s important to realize that when titanium(IV) chloride and water react, the reactants don’t actually decompose to their elements, which then recombine to form the products.
– But that is the great usefulness of Hess’s law and the state-function concept. Because ΔH°rxn is the difference between two state functions, ΔH°products minus ΔH°reactants, it doesn’t matter how the change actually occurs.
– We simply add the individual enthalpy changes to find ΔH°rxn:
– By generalizing the result shown here, we see that the standard heat of reaction is the sum of the standard heats of formation of the products minus the sum of the standard heats of formation of the reactants (see Figure above):
– where the symbol ∑ means “sum of,” and m and n are the amounts (mol) of the products and reactants indicated by the coefficients from the balanced equation.
Solved Problem on Standard Heats of Reaction (ΔH°rxn)
Nitric acid, whose worldwide annual production is nearly 10 billion kilograms, is used to make many products, including fertilizers, dyes, and explosives. The first step in the production process is the oxidation of ammonia:
Calculate ΔH°rxn from ΔH°f values.
Solution:
Calculating ΔH°rxn:
Check:
– One way to check is to write formation equations for the amounts of individual compounds in the correct direction and take their sum:
Comment:
– In this problem, we know the individual ΔH°f values and find the sum, ΔH°rxn.
– In the follow-up problem, we know the sum and want to find an individual value.
References
- Principles of Inorganic Chemistry / Brian W. Pfennig / 1st ed, 2015 /John Wiley & Sons, Inc/ USA.
- Principles of general Chemistry / Martin S. Silberberg / 2nd ed, 2010 /The McGraw-Hill Companies, Inc./ USA.
- Inorganic Chemistry /Peter Atkins, Tina Overton, Jonathan Rourkel, Mark Weller, Fraser Armstrong, Mike Hagerman / 6th ed, 2014 /W. H. Freeman and Company/ New York, USA.
-