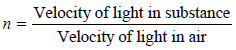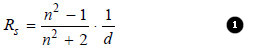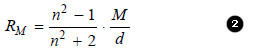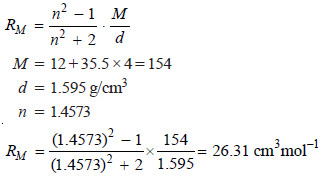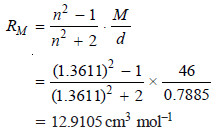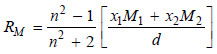Determination of Refractive Index
Refractive Index
– The refractive index (n) of a substance is defined as the ratio of the velocity of light in vacuum or air, to that in the substance:
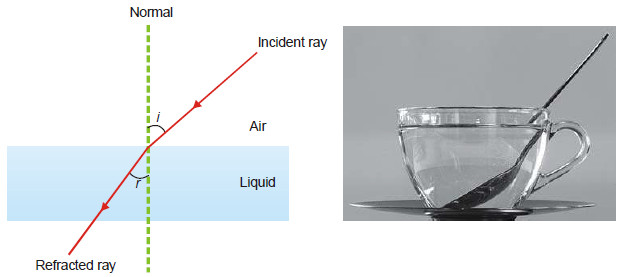
– When a ray of light passes from air into a liquid, its direction is changed. This change of direction is called refraction.
– The refractive index of the liquid with respect to air is given by Snelle’s Law.
According to it,
where (i) is the angle of incidence and r the angle of refraction.
– The refractive index of a liquid can be easily determined to a high degree of accuracy. It is a characteristic property of a liquid. It varies with temperature and wavelength of light used.
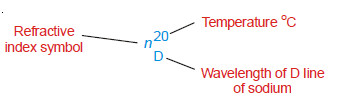
– The wavelength of D-line of the sodium spectrum is generally used for the purpose. If the refractive index of a liquid is measured at 20ºC and using D-line of sodium, it is represented by the following symbol.
Because refractive index is a ratio, it has no units.
Specific Refraction
– Lorenz and Lorenz (1880) purely from theoretical considerations derived the following relation for the refractive power of substance.
where:
Rs = the Specific Refraction,
d = the density,
n = the refractive index.
The value of Rs was constant at all temperatures.
Molar Refraction
– It is defined as the product of specific refraction and molecular mass.
– Thus molar refraction of a liquid (RM) is obtained by multiplying equation (1) by molecular mass (M).
– The value of molar refraction is characteristic of a substance and is temperature-independent.
– It can be determined by substituting the values of (n) , (M) and (d) in the equation (2).
– Since it depends on the wavelength of light, the values of molar refraction are generally reported for D-line of sodium.
– Since the value of refractive index (n) is dimensionless, from equation (2) it is evident that (RM) has the units of the molar volume i.e., cm3 mol–1.
Solved problems on refractive index
The refractive index of carbon tetrachloride for D-line of sodium has been found to be 1.4573. Calculate its molar refraction if the density is 1.595 g/cm3?
SOLUTION
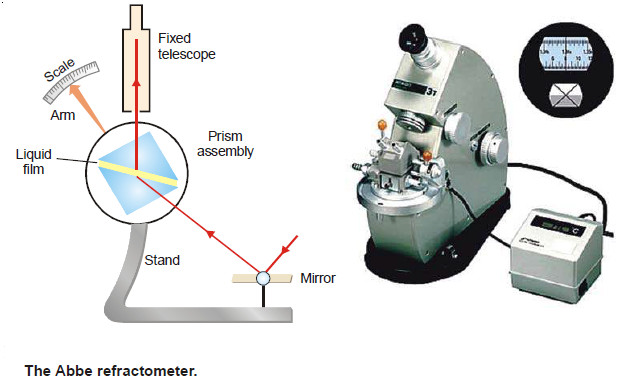
Determination of Refractive Index
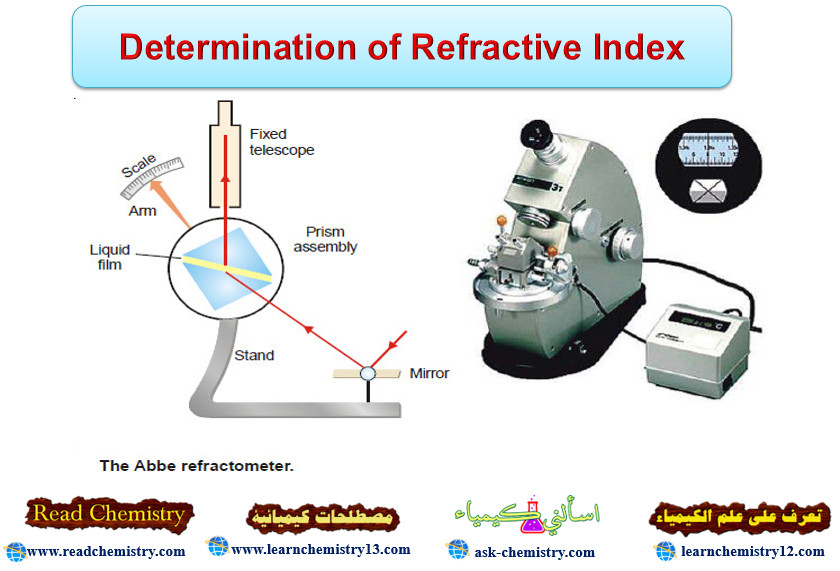
– The refractive index of a liquid can be determined with the help of an instrument called Abbe Refractometer.
– A thin film of the liquid is placed between the two prisms.
– Light from a sodium lamp is made to fall on lower side of the lower prism with the help of a mirror.
– The hypotenuse surface of the lower prism is ground and, therefore, light enters the liquid at all angles of incidence.
– However, no ray can enter the upper prism with greater angle of refraction than the grazing incidence (i.e., at an angle) slightly less than 90ºC.
– Thus the view in the telescope appears to be divided into two bands, one bright and one dark.
– The prism assembly is rotated with the help of a side knob till the cross wire of the telescope coincides with the edge of the bright band.
– A pointer attached to the prism assembly indicates the refractive index on the scale calibrated to read refractive indices directly.
Molar Refraction and Chemical Constitution
– The molar refraction (RM) is an additive property i.e. molar refraction of a molecule is the sum of the molar refraction of its constituent atoms.
– It is helpful in determining the constitution of a compound. The molar refraction values are calculated for various possible structures and the formula which is in accordance with the calculated molar refraction is the correct formula (or structure) of that compound.
– The molar refraction values for some atoms and bonds are given in following Table:
– Let us take the example of ethyl alcohol (CH3CH2OH). Its refractive index at 295.9 K for D-line is 1.3611 and its density is 0.7885 g cm–3. The molar mass of ethyl alcohol is 46 (2 × 12 + 1 × 6 + 1 × 16).
– The molar refraction can be calculated using the relation:
– Let us now compute the value of molar refraction using the values in the previous Table
Contribution of 6 Hydrogens = 6 × 1.100 = 6.600
and Contribution of 2 Carbons = 2 × 2.418 = 4.836
Contribution of O in OH group = 1.525
Total contribution = 12.961 cm3 mol–1
– This value is in close agreement with the value calculated above. Therefore, the correct structure of ethyl alcohol is CH3CH2OH.
The molar refraction RM of a solution is given by:
where:
x1 and x2 = mole fractions of the solvent and solute with molecular masses M1 and M2 respectively,
n = is the refractive index of the solution,
d = is the density of the solution.