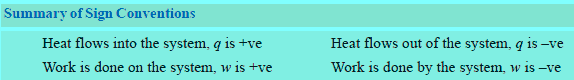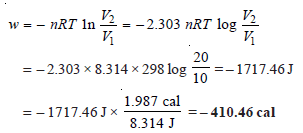Work in Thermodynamics (Definition – Formula – Problems)

– In physics, mechanical work is defined as force multiplied by the distance through which the force acts.

– In elementary thermodynamics, the only type of work generally considered is the work done in the expansion (or compression) of a gas

Nature of Heat and Work

 – When a change in the state of a system occurs, energy is transferred to or from the surroundings.

– This energy may be transferred as heat or mechanical work.

– We shall refer to the term ‘work’ for mechanical work which is defined as: force × distance.

Work = force × distance

Units of Work

– In the CGS system the unit of work is erg

– Erg is the work done when a resistance of 1 dyne is moved through a distance of 1 centimeter.

– Since the erg is so small, a bigger unit, the joule (J) is now used.

1 joule = 10⁷ ergs

1 erg = 10^–7 J

– We often use kilojoules (kJ) for large quantities of work:

1 kJ = 1000 J

Units of Heat

– The unit of heat, which was used for many years, is calorie (cal).

– A calorie: is the quantity of heat required to raise the temperature of 1 gram of water by 1º C in the vicinity of 15ºC.

– Since heat and work are interrelated, the SI unit of heat is the joule (J).

1 joule = 0.2390 calories

but 1 calorie = 4.184 J

1 kcal = 4.184 kJ

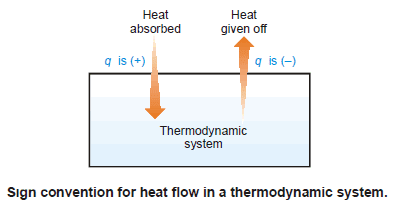
Sign Convention of Heat

– The symbol of heat is q.

– If the heat flows from the surroundings into the system to raise the energy of the system, it is taken to be positive, +q.

– If heat flows from the system into the surroundings, lowering the energy of the system, it is taken to be negative, –q.

Sign Convention of Work

– The symbol of work is w.

– If work is done on a system by the surroundings and the energy of the system is thus increased, it is taken to be positive, +w.

– If work is done by the system on the surroundings and the energy of the system is decreased, it is taken to be negative, –w.

Pressure-Volume Work

– In physics, mechanical work is defined as force multiplied by the distance through which the force acts.

– In elementary thermodynamics, the only type of work generally considered is the work done in the expansion (or compression) of a gas.

– This is known as pressure-volume work or PV work or expansion work.

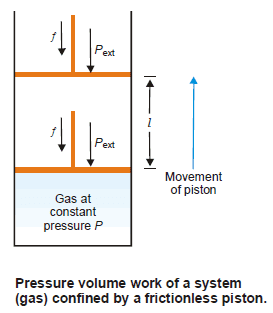
– Consider a gas contained in a cylinder fitted with a frictionless piston.

– The pressure (force per unit area) of the gas, P, exerts a force on the piston.

– This can be balanced by applying an equal but opposite pressure from outside on the piston.

Explanation of Pressure-Volume Work

– Let it be designated as P_ext.

– It is important to remember that it is the external pressure, P_ext. and not the internal pressure of the gas itself which is used in evaluating work.

– This is true whether it be expansion or contraction.

– If the gas expands at constant pressure, the piston would move, say through a distance l.

– We know that:

work = force × distance (by definition)

w = f × l        …….(1)

– Since pressure is force per unit area,

f = P_ext × A        …….(2)

 

– where A is the cross-section area of the piston.

– From (1) and (2), we have

w = P_ext × A × l

= P_ext× ΔV

– where ΔV is the increase in the volume of the gas

– Since the system (gas) is doing work on the surroundings (piston), it bears a negative sign. Thus,

w = –P_ext × ΔV

Proceeding as above the work done in compression of a gas can also be calculated. In that case, the piston will move down and the sign of the work will be positive.

w = P_ext × ΔV

– As already stated, work may be expressed in dynes-centimeters, ergs, or joules. PV work can also be expressed as the product of pressure and volume units e.g., in litres or atmospheres.

– It may be noted that the work done by a system is not a state function.

– This is true of the mechanical work of expansion.

– We shall show presently that the work is related to the process carried out rather than to the internal and final states.

– This will be evident from a consideration of the reversible expansion and an irreversible process.

Solved Problem

Calculate the pressure-volume work done when a system containing a gas expands from 1.0 liter to 2.0 liters against a constant external pressure of 10 atmospheres. Express the answer in calories and joules.

Solution:

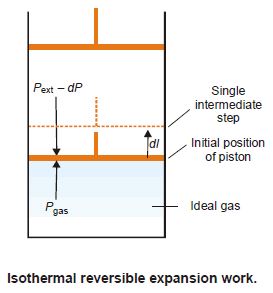
Isothermal Reversible Expansion Work of an Ideal Gas

– Consider an ideal gas confined in a cylinder with a frictionless piston.

– Suppose it expands in a reversible manner from volume V₁ to V₂ at a constant temperature.

– The pressure of the gas is successively reduced from P₁ to P₂.

– The reversible expansion of the gas takes place in a finite number of infinitesimally small intermediate steps.

– To start with the external pressure, P_ext, is arranged equal to the internal pressure of the gas, P_gas, and the piston remains stationary.

– If P_ext is decreased by an infinitesimal amount dP the gas expands reversibly and the piston moves through a distance dl.

– Since dP is so small, for all practical purposes,

P_ext= P_gas = P

– The work done by the gas in one infinitesimal step dw, can be expressed as:

(A = cross-sectional area of piston)

dw = P × A × dl

= P × dV

– where dV is the increase in volume

– The total amount of work done by the isothermal reversible expansion of the ideal gas from V₁ to V₂ is, therefore:

– Isothermal compression work of an ideal gas may be derived similarly and it has exactly the same value with the sign changed.

– Here the pressure on the piston, P_ext, is increased by dP which reduces the volume of the gas.

Isothermal Irreversible Expansion Work of an Ideal Gas

– Suppose we have an ideal gas contained in a cylinder with a piston.

– This time the process of expansion of the gas is performed irreversibly i.e., by instantaneously dropping the external pressure, P_ext, to the final pressure P₂.

– The work done by the system is now against the pressure P₂ throughout the whole expansion and is given by the following expression:

Maximum Work done in Reversible Expansion

– The isothermal expansion of an ideal gas may be carried either by the reversible process or irreversible process as stated above.

– The reversible expansion is shown in the following figure in which the pressure falls as the volume increases.

– The reversible work done by the gas is given by the expression:

 

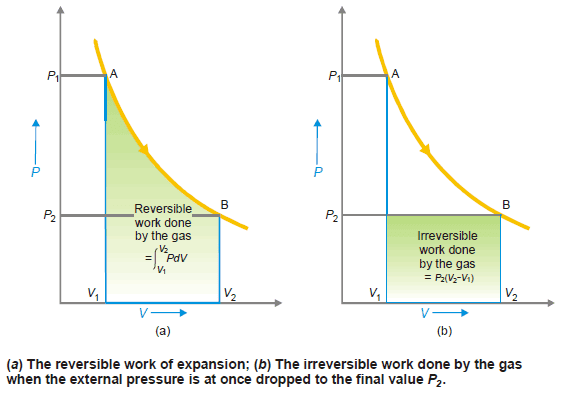
which is represented by the shaded area.

– If the expansion is performed irreversibly by suddenly reducing the external pressure to the final pressure P₂, the irreversible work is given by:

– w_in= P₂ (V₂ – V₁)

which is shown by the shaded area in Fig (b).

– In both the processes, the state of the system has changed from A to B but the work done is much less in the irreversible expansion than in the reversible expansion.

– Thus mechanical work is not a state function as it depends on the path by which the process is performed rather than on the initial and final states. It is a path function.

Maximum work

– It is also important to note that the work done in the reversible expansion of a gas is the maximum work that can be done by a system (gas) in expansion between the same initial (A) and final state (B).

• This is proved as follows :

– We know that the work always depends on the external pressure, P_ext; the larger the P_ext the more work is done by the gas.

– But the P_ext on the gas cannot be more than the pressure of the gas, P_gas or compression will take place.

– Thus the largest value P_ext can have without a compression taking place is equal to P_gas.

– But an expansion that occurs under these conditions is the reversible expansion.

– Thus, maximum work is done in the reversible expansion of a gas.

Solved Problem

Problem (1): One mole of an ideal gas at 25ºC is allowed to expand reversibly at constant temperature from a volume of 10 liters to 20 liters. Calculate the work done by the gas in joules and calories.

Solution:

Problem (2): Find the work done when one mole of the gas is expanded reversibly and isothermally from 5 atm to 1 atm at 25ºC.

Solution:

Reference: Essentials of Physical Chemistry /Arun Bahl, B.S Bahl and G.D. Tuli / multicolor edition.