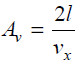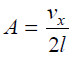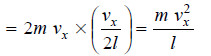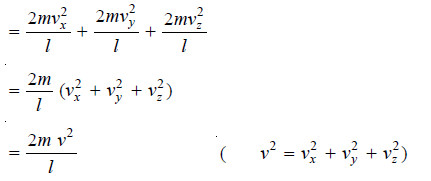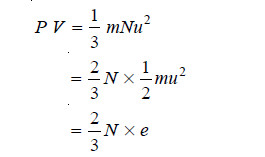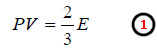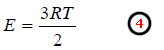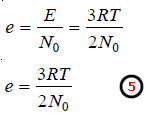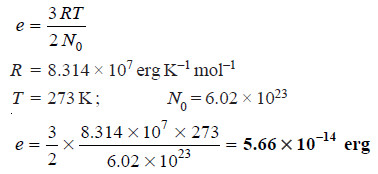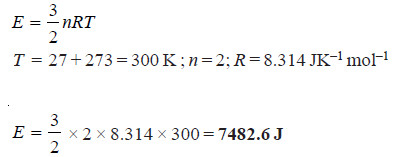Derivation of the Kinetic Gas Equation

– In this topic, we will talk aboutDerivation of the Kinetic Gas Equation.

Derivation of the Kinetic Gas Equation

– Starting from the postulates of the kinetic molecular theory of gases we can develop an important equation.

– This equation expresses PV of a gas in terms of the number of molecules, molecular mass and molecular velocity.

– This equation which we shall name as the Kinetic Gas Equation may be derived by the following clauses.

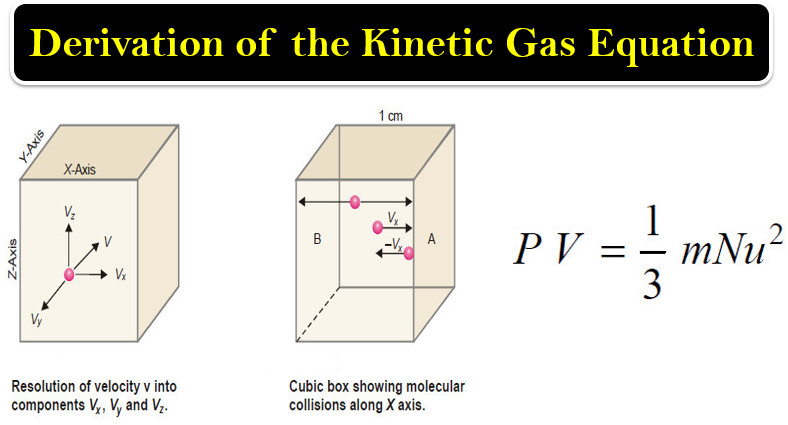
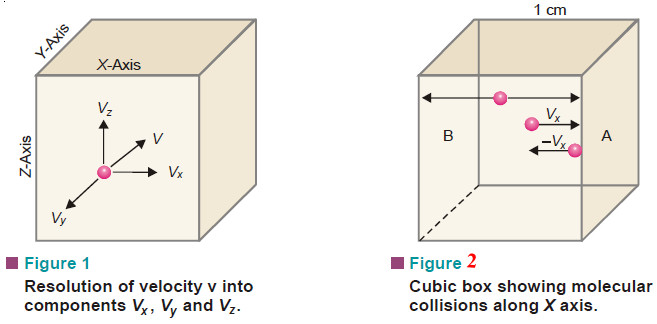
– Let us consider a certain mass of gas enclosed in a cubic box (Fig.1) at a fixed temperature.

– Suppose that :

the length of each side of the box = l cm

the total number of gas molecules = n

the mass of one molecule = m

the velocity of a molecule = v

– The kinetic gas equation may be derived by the following steps :

(1) Resolution of Velocity v of a Single Molecule Along X, Y and Z Axes

– According to the kinetic theory, a molecule of a gas can move with velocity v in any direction.

– Velocity is a vector quantity and can be resolved into the components v_x, v_y, v_z along the X, Y and Z axes.

– These components are related to the velocity v by the following expression.

– Now we can consider the motion of a single molecule moving with the component velocities independently in each direction.

(2) The Number of Collisions Per Second on Face A Due to One Molecule

– Consider a molecule moving in OX direction between opposite faces A and B.

– It will strike the face A with velocity v_x and rebound with velocity – v_x.

– To hit the same face again, the molecule must travel l cm to collide with the opposite face B and then again l cm to return to face A.

– Therefore,

the time between two collisions of face seconds

the number of collisions per second on face

(3) The Total Change of Momentum on All Faces of the Box Due to One Molecule Only

– Each impact of the molecule on the face A causes a change of momentum (mass × velocity):

the momentum before the impact = mv_x

the momentum after the impact = m (– v_x)

∴ the change of momentum = mv_x – (– mv_x) = 2 mv_x

– But the number of collisions per second on face A due to one molecule =

– Therefore, the total change of momentum per second on face A caused by one molecule

– The change of momentum on both the opposite faces A and B along X-axis would be double i.e.,

– similarly, the change of momentum along Y-axis and Z-axis will be respectively.

– Hence, the overall change of momentum per second on all faces of the box will be:

(4) Total Change of Momentum Due to Impacts of All the Molecules on All Faces of the Box

– Suppose there are N molecules in the box each of which is moving with a different velocity v₁, v₂, v₃, etc.

– The total change of momentum due to impacts of all the molecules on all faces of the box

– Multiplying and dividing by n, we have:

where u² is the mean square velocity.

(5) Calculation of Pressure from Change of Momentum; Derivation of Kinetic Gas Equation

– Since force may be defined as the change in momentum per second, we can write:

– This is the fundamental equation of the kinetic molecular theory of gases. It is called the Kinetic Gas equation.

– This equation although derived for a cubical vessel, is equally valid for a vessel of any shape.

– The available volume in the vessel could well be considered as made up of a large number of infinitesimally small cubes for each of which the equation holds.

– Significance of the term u. As stated in clause (4) u² is the mean of the squares of the individual velocities of all the N molecules of the gas. But .

– Therefore u is called the Root Mean Square (or RMS) Velocity.

Kinetic Gas Equation in terms of kinetic energy

– If N be the number of molecules in a given mass of gas,

where e is the average kinetic energy of a single molecule.

or

– where E is the total kinetic energy of all the N molecules.

– The expression (1) may be called the kinetic gas equation in terms of kinetic energy.

– We know that the General ideal gas equation is:

– From (1) and (2):

– For one mole of gas, the kinetic energy of N molecules is,

– Since the number of gas molecules in one mole of gas in N₀ (Avogadro number),

– substituting the values of R, T, N₀, in the equation (5), the average kinetic energy of a gas molecule can be calculated.

Solved problem on Derivation of the Kinetic Gas Equation

Problem (1): Calculate the average kinetic energy of a hydrogen molecule at 0°C.

Solution:

– Thus the average kinetic energy of H2 at 0°C is 5.66 × 10–14 erg

Problem (2): Calculate the kinetic energy of two moles of N2 at 27°C. (R = 8.314 JK^–1)

Solution:

– Therefore the kinetic energy of two moles of N₂ is 7482.6 J.

References