Calculation of Kc from Experimental Information

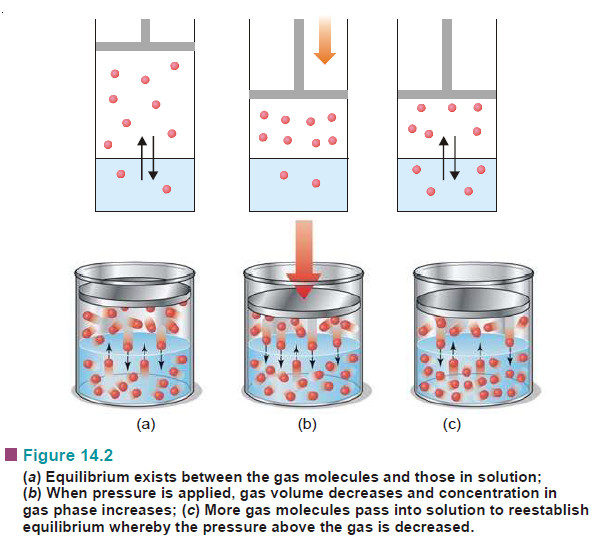
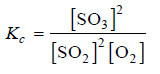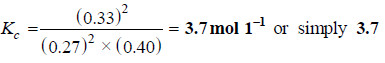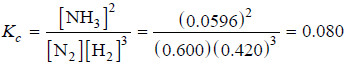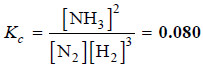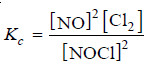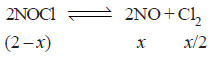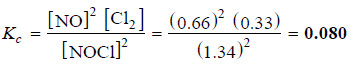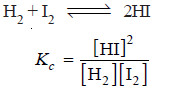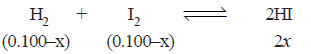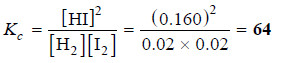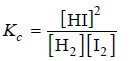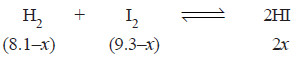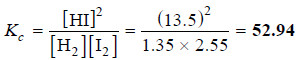Calculation of K_c from Experimental Information

– To determine the value of K_c of a reaction, write the balanced equation. Then write the equilibrium constant expression.

– Substitute in it the equilibrium concentrations of the reactants and products found experimentally. Thus calculate the value of K_c.

Solved problem (1) for Calculation of K_c

At equilibrium for the reaction:

2SO_2(g) + O_{2 (g)} ↔ 2SO_{3 (g)}

the concentrations of reactants and products at 727°C were found to be: SO₂ = 0.27 mol L^–1; O₂ = 0.40 mol L^–1; and SO₃ = 0.33 mol L^-1. What is the value of the equilibrium constant, K_c, at this temperature?

Solution:

– Write the equilibrium constant expression for the reaction:

– We know that:

[SO₃] = 0.33 mol L^–1; [SO₂] = 0.27 mol L^–1; [O₂] = 0.40 mol L^–1

– Substituting these values in the equilibrium constant expression, we have:

Solved problem (2)

Some nitrogen and hydrogen gases are pumped into an empty five litre glass bulb at 500°C. When equilibrium is established, 3.00 moles of N₂, 2.10 moles of H₂ and 0.298 mole of NH₃ are found to be present. Find the value of K_c for the reaction.

N_2(g) + 3H_2(g) ↔ 2NH_3(g)

at 500°C.

Solution:

– The equilibrium concentrations are obtained by dividing the number of moles of each reactant and product by the volume, 5.00 litres. Thus,

[N₂] = 3.00 mole/5.00 L = 0.600 M

[H₂] = 2.10 mole/5.00 L = 0.420 M

[NH₃] = 0.298 mole/5.00 L = 0.0596 M

– Substituting these concentrations (not number of moles) in the equilibrium constant expression, we get the value of K_c.

– Thus, for the reaction of H₂ and N₂ to form NH₃ at 500°C, we can write:

Solved problem (3)

Calculate the equilibrium constant at 25°C for the reaction:

2NOCl_(g) ↔ 2NO_(g) + Cl_{2 (g)}

In an experiment, 2.00 moles of NOCl were placed in a one-litre flask and the concentration of NO after equilibrium achieved was 0.66 mole/litre.

Solution:

– Let us write the equilibrium constant expression for the balanced chemical equation.

– Next we proceed to find the equilibrium concentrations of NOCl, NO and Cl₂.

– Since the volume of the reaction vessel is one litre, the moles of various reagents also represent their molar concentrations.

– The initial amount of NOCl is 2.00 moles.

– Let us assume that x moles of it have reacted to achieve the equilibrium.

– The moles of different reagents at equilibrium are indicated in the equation.

– According to this equation, one mole of NOCl gives one mole of NO and half a mole of Cl₂.

– The experimental value of equilibrium concentration of NO is 0.66 mole/litre.

– Therefore, the equilibrium concentration Cl₂ is half of it i.e. 0.33 mole/litre. Since x = 0.66, the equilibrium concentration of NOCl = (2 – 0.66) = 1.34. To find K_c , these values of equilibrium concentrations are substituted in the equilibrium constant expression.

Solved problem (4)

At a certain temperature, 0.100 mole of H₂ and 0.100 mole of I₂ were placed in a one-litre flask. The purple colour of iodine vapour was used to monitor the reaction. After a time, the equilibrium

H₂ + I₂ ↔ 2HI

was established and it was found that the concentration of I₂ decreased to 0.020 mole/litre.

Calculate the value of K_c for the reaction at the given temperature.

Solution:

– The equilibrium constant expression for the reaction:

– Let us proceed to find the equilibrium concentrations of the various species.

– The initial moles of H₂ , I₂ and HI present at equilibrium are:

moles at equilibrium

– Since the volume of the reaction vessel is one litre, the moles at equilibrium also represent the equilibrium concentrations. Thus,

[I₂] = 0.100 – x = 0.020 (given)

or   x = 0.100 – 0.020

= 0.080

– Knowing the value of x, we can give the equilibrium concentrations of H₂ , I₂ and HI.

[H₂] = 0.100 – x = 0.100 – 0.080 = 0.020

[I₂] = 0.020 (given)

[HI] = 2x = 0.160

– Substituting these values in the equilibrium constant expression, we get the value of K_c.

Solved problem (5)

13.5 ml of HI are produced by the interaction of 8.1 ml of hydrogen and 9.3 ml of iodine vapour at 444°C. Calculate the equilibrium constant at this temperature of the reaction.

H_2(g) + I_{2 (g)} ↔ 2HI _(g)

Solution:

– The equilibrium constant expression for the reaction is:

– Let us proceed to find the equilibrium concentrations.

– Since the number of moles in a gas under the same conditions of temperature and pressure are proportional to volumes, ml of a gas may be used instead of molar concentrations. Thus,

– The experimental volume of HI = 13.5 ml (given)

∴ 2x = 13.5 ml

or   x = 6.75 ml

– Thus, the equilibrium concentrations are:

[H₂] = (8.1 – x) = 8.1 – 6.75 = 1.35

[I₂] = (9.3 – x) = 9.3 – 6.75 = 2.55

[HI] = 13.5

– Substituting these values in the equilibrium constant expression, we have: