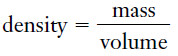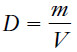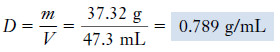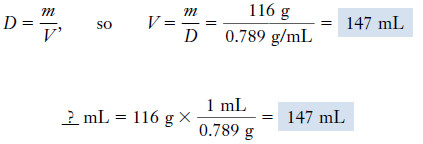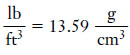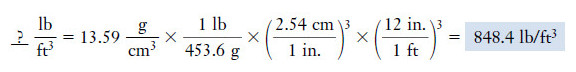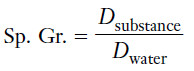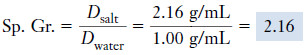Density and Specific gravity: Definition, Solved problems
– In this topic, we will discuss The Density and Specific gravity: Definition and Solved problems.
Definition of Density
– In science, we use many terms that involve combinations of different units.
– Such quantities may be thought of as unit factors that can be used to convert among these units.
– The density of a sample of matter is defined as the mass per unit volume.
– Densities may be used to distinguish between two substances or to assist in identifying a particular substance.
– They are usually expressed as g/cm3 or g/mL for liquids and solids and as g/L for gases.
– These units can also be expressed as g.cm-3, g.mL-1, and g.L-1, respectively.
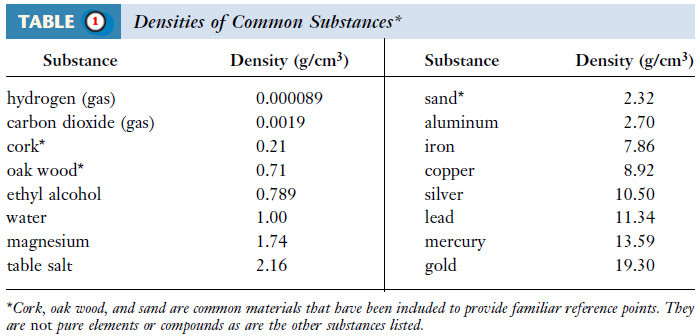
– Densities of several substances are listed in the following Table (1):
Solved Problems on density
Example (1): A 47.3-mL sample of ethyl alcohol (ethanol) has a mass of 37.32 g. What is its density?
Plan
– We use the definition of density.
Solution:
Example (2): If 116 g of ethanol is needed for a chemical reaction, what volume of liquid would you use?
Plan
– We determined the density of ethanol in Example (1).
– Here we are given the mass, m, of a sample of ethanol.
– So we know values for D and m in the relationship:
– We rearrange this relationship to solve for V, put in the known values, and carry out the calculation.
– Alternatively, we can use the unit factor method to solve the problem.
Solution
The density of ethanol is 0.789 g/mL (Table 1).
Example (3): Unit Conversion Express the density of mercury in lb/ft3.
Plan
– The density of mercury is 13.59 g/cm3 (see Table 1).
– To convert this value to the desired units, we can use unit factors constructed from the conversion factors as follow:
Solution
– It would take a very strong person to lift a cubic foot of mercury!
Definition of Specific gravity
– The specific gravity (Sp. Gr.) of a substance is the ratio of its density to the density of water, both at the same temperature.
– The density of water is 1.000 g/mL at 3.98°C, the temperature at which the density of water is greatest.
– Variations in the density of water with changes in temperature, however, are small enough that we can use 1.00 g/mL up to 25°C without introducing significant errors into our calculations.
Solved Problems on Specific Gravity
Example (4): The density of table salt is 2.16 g/mL at 20°C. What is its specific gravity?
Plan
– We use the preceding definition of specific gravity.
– The numerator and denominator have the same units, so the result is dimensionless.
Solution
– This example also demonstrates that the density and specific gravity of a substance are numerically equal near room temperature if density is expressed in g/mL (g/cm3).
– Labels on commercial solutions of acids give specific gravities and the percentage by mass of the acid present in the solution.
– From this information, the amount of acid present in a given volume of solution can be calculated.
Example (5): Battery acid is 40.0% sulfuric acid, H2SO4, and 60.0% water by mass. Its specific gravity is 1.31. Calculate the mass of pure H2SO4 in 100.0 mL of battery acid.
Plan
– The percentages are given on a mass basis, so we must first convert the 100.0 mL of acid solution (soln) to mass.
– To do this, we need a value for the density.
– We have demonstrated that density and specific gravity are numerically equal at 20°C because the density of water is 1.00 g/mL.
– We can use the density as a unit factor to convert the given volume of the solution to mass of the solution.
– Then we use the percentage by mass to convert the mass of the solution to the mass of the acid.
Solution
– From the given value for specific gravity, we may write:
Density = 1.31 g/mL
– The solution is 40.0% H2SO4 and 60.0% H2O by mass.
– From this information we may construct the desired unit factor:
References:
- Principles of Inorganic Chemistry / Brian W. Pfennig / 1st ed, 2015 /John Wiley & Sons, Inc/ USA.
- Inorganic Chemistry /Peter Atkins, Tina Overton, Jonathan Rourkel, Mark Weller, Fraser Armstrong, Mike Hagerman / 6th ed, 2014 /W. H. Freeman and Company/ New York, USA.
-