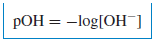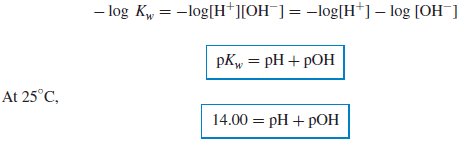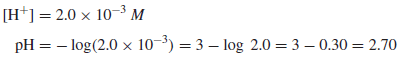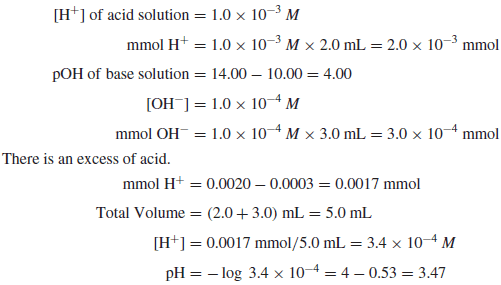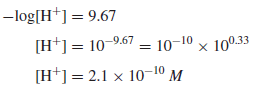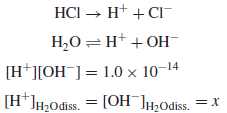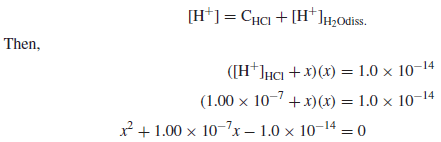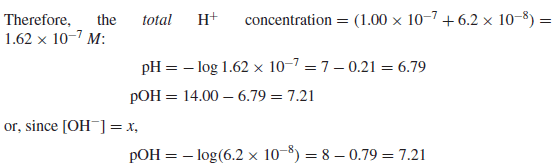pH Scale: Definition, formula, Notes, Solved problems
– In this subject, we will discuss the pH Scale: Definition, formula, Notes, Solved problems
pH Scale
– The concentration of H+ or OH− in aqueous solution can vary over extremely wide ranges, from 1 M or greater to 10−14 M or less.
– To construct a plot of H+ concentration against some variable would be very difficult if the concentration changed from, say, 10−1 M to 10−13 M.
– This range is common in titration.
– It is more convenient to compress the acidity scale by placing it on a logarithm basis.
– The pH of a solution was defined by Sørenson as:
– The minus sign is used because most of the concentrations encountered are less than 1 M, and so this designation gives a positive number. (More strictly, pH is now defined as −log aH+, but we will use the simpler definition of Equation above)
– In general, pAnything = −log Anything, and this method of notation will be used later for other numbers that can vary by large amounts, or are very large or small (e.g., equilibrium constants).
– Carlsberg Laboratory archives In 1909, Søren Sørenson, head of the chemistry department at Carlsberg Laboratory (Carlsberg Brewery) invented the term pH to describe this effect and defined it as −log[H+].
– The term pH refers simply to (the power of hydrogen).
– In 1924, Søren Sørenson realized that the pH of a solution is a function of the (activity) of the H+ ion, and published a second paper on the subject, defining it as pH = −log aH+.
– A similar definition is made for the hydroxide ion concentration:
So
Solved Problems
Example (1): Calculate the pH of a 2.0 × 10−3 M solution of HCl.
Solution:
HCl is completely ionized, so
Example (2): Calculate the pOH and the pH of a 5.0 × 10−2 M solution of NaOH at 25◦C.
Solution:
Example (3): Calculate the pH of a solution prepared by mixing 2.0mL of a strong acid solution of pH 3.00 and 3.0mL of a strong base of pH 10.00.
Solution:
Example (4): The pH of a solution is 9.67. Calculate the hydrogen ion concentration in the solution
Solution:
Important Notes for pH
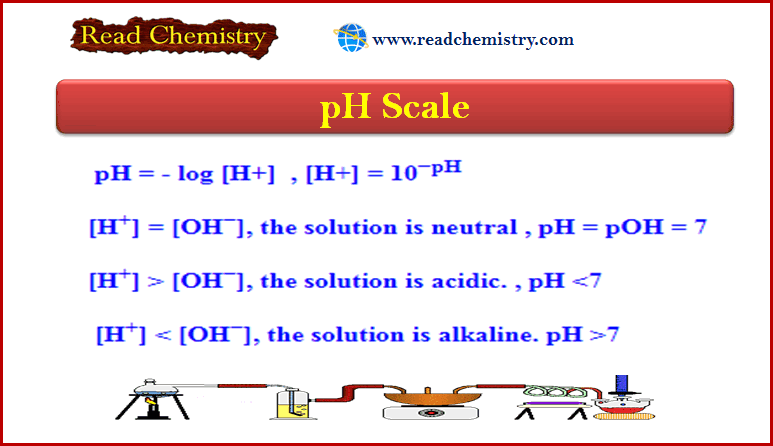
pH = – log [H+] → [H+] = 10−pH
If [H+] = [OH−] → The solution is Neutral → pH = pOH = 7
[H+] > [OH−] → The solution is Acidic → pH <7
[H+] < [OH−] → The solution is Alkaline → pH >7
– The hydrogen ion and hydroxide ion concentrations in pure water at 25◦C are each 10−7 M, and the pH of water is 7. A pH of 7 is therefore neutral.
– Values of pH that are greater than this are alkaline, and pH values less than this are acidic.
– The reverse is true of pOH values. A pOH of 7 is also neutral.
– Note that the product of [H+] and [OH−] is always 10−14 at 25◦C, and the sum of pH and pOH is always 14.
– If the temperature is other than 25◦C, then Kw is different from 1.0 × 10−14, and a neutral solution will have other than 10−7 M H+ and OH− (see below).
– If the concentration of an acid or base is much less than 10−7 M, then its contribution to the acidity or basicity will be negligible compared with the contribution from water.
– The pH of a 10−8 M sodium hydroxide solution would therefore not differ significantly from 7.
– If the concentration of the acid or base is around 10−7 M, then its contribution is not negligible and neither is that from water; hence the sum of the two contributions must be taken. So,
The pH of 10-9 M HCl is not 9!
Negative pH
– Some mistakenly believe that it is impossible to have a negative pH. There is no theoretical basis for this.
– A negative pH only means that the hydrogen ion concentration is greater than 1 M.
– In actual practice, a negative pH is uncommon for two reasons:
(1) The First reason:
– even strong acids may become partially undissociated at high concentrations.
– For example, 100% H2SO4 is so weakly dissociated that it can be stored in iron containers; more dilute H2SO4 solutions would contain sufficient protons from dissociation to attack and dissolve the iron.
(2) The second reason:
– It has to do with the activity, which we have chosen to neglect for dilute solutions.
– Since pH is −log aH+ (this is what a pH meter reading is a measure of), a solution that is 1.1 M in H+ may actually have a positive pH because the activity of the H+ is less than 1.0 M.
– This is because, at these high concentrations, the activity coefficient is less than unity (although at still higher concentrations the activity coefficient may become greater than unity).
– Nevertheless, there is mathematically no basis for not having a negative pH (or a negative pOH), although it may be rarely encountered in situations relevant to analytical chemistry.
– Example: 10 M HCl solution should have a pH of −1 and pOH of 15
Solved Problem
Calculate the pH and pOH of a 1.0 × 10−7 M solution of HCl.
Solution:
– Since the hydrogen ions contributed from the ionization of water are not negligible compared to the HCl added
– Note that owing to the presence of the added H+, the ionization of water is suppressed by 38% by the common ion effect (Le Chˆatelier’s principle).
– At higher acid (or base) concentrations, the suppression is even greater and the contribution from the water becomes negligible.
– The contribution from the autoionization of water can be considered negligible if the concentration of protons or hydroxyl ions from an acid or base is 10−6 M or greater.
– The calculation in this example is more academic than practical because carbon dioxide from the air dissolved in water substantially exceeds these concentrations, being about 1.2 × 10−5 M carbonic acid.
– Since carbon dioxide in water forms an acid, extreme care would have to be taken to remove and keep this from the water, to have a solution of 10−7 M acid.
Reference: Analytical chemistry/ Seventh edition / Gary D. Christian, University of Washington, Purnendu K. (Sandy) Dasgupta, University of Texas at Arlington, Kevin A. Schug, University of Texas at Arlington.