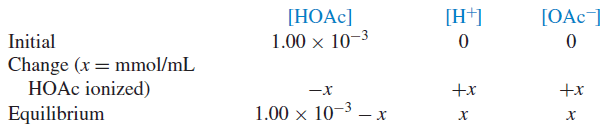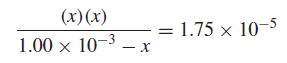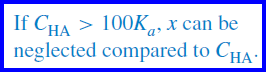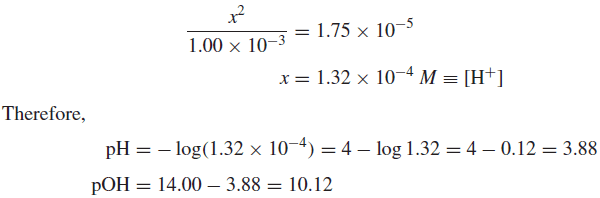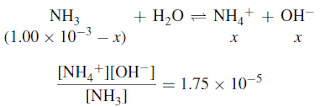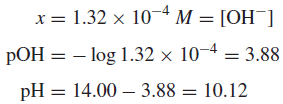Calculating the pH of Weak Acid and Base Solutions
– In this subject, we will discuss Calculating the pH of Weak Acid and Base Solutions

Total and partial ionization
– When an acid or base is dissolved in water, it will dissociate, or ionize According to the equations:
– The amount of ionization is dependent on the strength of the acid or the base.
– A strong electrolyte is completely dissociated, while a weak electrolyte is partially dissociated.
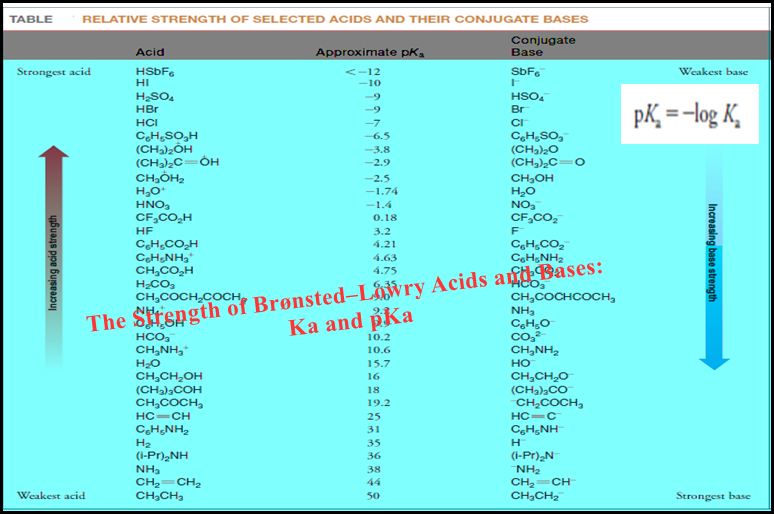
– The table below shows lists some common electrolytes, some strong and some weak:
– Hydrochloric acid is a strong acid, and in water, its ionization is complete:
– Acetic acid is a weak acid, which ionizes only partially in water (a few percent):
Calculating the pH of Weak Acid
– Acetic acid is a weak acid, which ionizes only partially in water (a few percent):
– The ionization constant can be used to calculate the amount ionized and, from this, the pH.
– The acidity constant for acetic acid at 25◦C is 1.75 × 10−5:
– When acetic acid ionizes, it dissociates to equal portions of H+ and OAc− by such an amount that the computation on the left side of the Equation above will always be equal to 1.75 × 10−5:
– If the original concentration of acetic acid is C and the concentration of ionized acetic acid species (H+ and OAc−) is x, then the final concentration for each species at equilibrium is given by:
Solved Problem for Calculating the pH of weak Acid
Example (1): Calculate the pH and pOH of a 1.00 × 10−3M solution of acetic acid.
Solution:
Note:
– The solution is that of a quadratic equation.
– If less than about 10 or 15% of the acid is ionized, the expression may be simplified by neglecting x compared with C (10−3 M in this case).
– This is an arbitrary (and not very demanding) criterion.
– The simplification applies if Ka is smaller than about 0.01C, that is, smaller than 10−4 at C = 0.01 M, 10−3 at C = 0.1 M, and so forth.
– Under these conditions, the calculation error is 5% or less (results come out too high), and within the probable accuracy of the equilibrium constant.
– Our calculation simplifies to:
– The simplification in the calculation does not lead to serious errors, particularly since equilibrium constants are often not known to a high degree of accuracy (frequently no better than ±10%).
– In the above example, the solution of the quadratic equation results in [H+] = 1.26 × 10−4 M (5% less) and pH = 3.91.
– This pH is within 0.03 units of that calculated using the simplification, which is near the limit of accuracy to which pH measurements can be made.
– It is almost certainly as close a calculation as is justified because of the experimental errors in Ka or Kb values and the fact that we are using concentrations rather than activities in the calculations.
– In our calculations, we also neglected the contribution of hydrogen ions from the ionization of water (which was justified); this is generally permissible except for very dilute (<10−6 M) or very weak (Ka < 10−12) acids.
Calculating the pH of Weak bases
– Ammonia is a weak base, which ionizes only partially in water:
– The ionization constant can be used to calculate the amount ionized and, from this, the pOH.
– The acidity constant for ammonia at 25◦C is 1.75 × 10−5:
Example (2): The basicity constant Kb for ammonia is 1.75 × 10−5 at 25◦C. (It is only coincidental that this is equal to Ka for acetic acid.) Calculate the pH and pOH for a 1.00 × 10−3 M solution of ammonia.
Solution:
Reference: Analytical chemistry/ Seventh edition / Gary D. Christian, University of Washington, Purnendu K. (Sandy) Dasgupta, University of Texas at Arlington, Kevin A. Schug, University of Texas at Arlington.