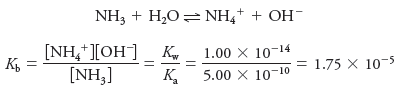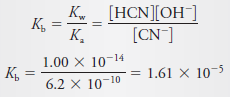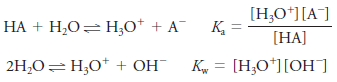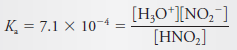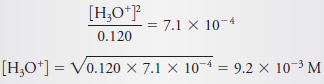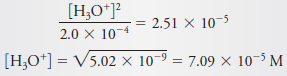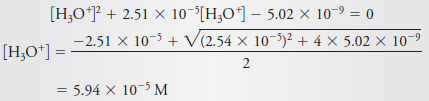Acid and Base Dissociation Constants (Ka and Kb)
– In this subject, we will discuss the Acid and Base Dissociation Constants (Ka and Kb)
Acid and Base Dissociation Constants
– When a weak acid or a weak base is dissolved in water, partial dissociation occurs.
– Thus, for nitrous acid, we can write:
– where Ka is the acid dissociation constant for nitrous acid.
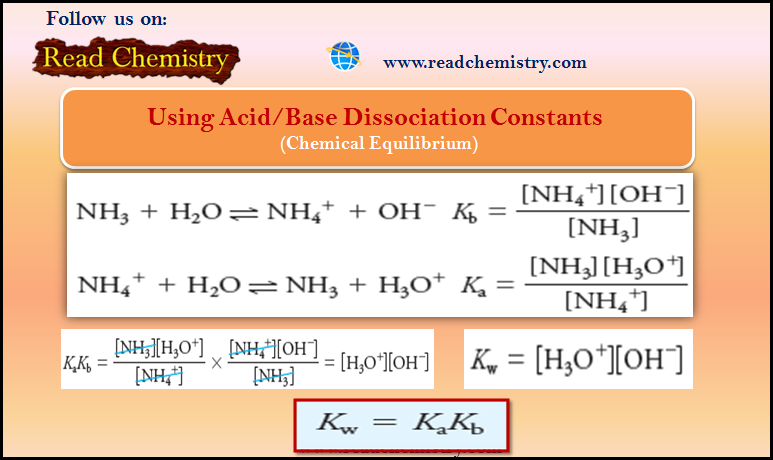
– Analogously, the base dissociation constant for ammonia is
– Notice that [H2O] does not appear in the denominator of either equation because the concentration of water is so large relative to the concentration of the weak acid or base that the dissociation does not alter [H2O] appreciably.
– Just as in the derivation of the ion-product constant for water, [H2O] is incorporated into the equilibrium constants Ka and Kb.
Dissociation Constants for Conjugate Acid / Base Pairs
– Consider the base dissociation-constant expression for ammonia and the acid dissociation constant expression for its conjugate acid, ammonium ion:
– By multiplying one equilibrium-constant expression by the other, we have:
but
and, therefore,
– This relationship is general for all conjugate acid/base pairs.
– Many compilations of equilibrium constant data list only acid dissociation constants because it is so easy to calculate dissociation constants for bases.
– For example, we find no data on the basic dissociation of ammonia (nor for any other bases).
– Instead, we find the acid dissociation constant for the conjugate acid, ammonium ion. That is,
– and we can write:
Solved problem (1) on Dissociation Constants
What is Kb for the equilibrium:
Solution:
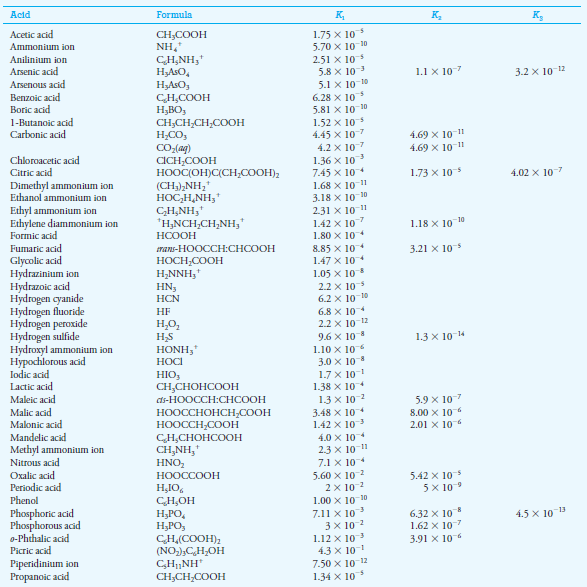
In the table below this subject, the Ka value of 6.2 × 10-10 for HCN. Thus,
Hydronium Ion Concentration of Solutions of Weak Acids
– When the weak acid HA is dissolved in water, two equilibria produce hydronium ions:
– Normally, the hydronium ions produced from the first reaction suppress the dissociation of water to such an extent that the contribution of hydronium ions from the second equilibrium is negligible.
– Under these circumstances, one H3O+ion is formed for each A– ion, and we write:
– Furthermore, the sum of the molar concentrations of the weak acid and its conjugate base must equal the analytical concentration of the acid cHA because the solution contains no other source of A– ions.
– Therefore,
– Substituting [H3O+] for [A–] (see Equation 2) in Equation (3) yields:
– which rearranges to
– When [A–] and [HA] are replaced by their equivalent terms from Equations (2) and (4), the equilibrium-constant expression becomes:
– which rearranges to
– The positive solution to this quadratic equation is
– Equation (4) can frequently be simplified by making the additional assumption that dissociation does not appreciably decrease the molar concentration of HA.
– Thus, if [H3O+] << cHA, cHA – [H3O+] ≈ cHA, and Equation (5) reduces to:
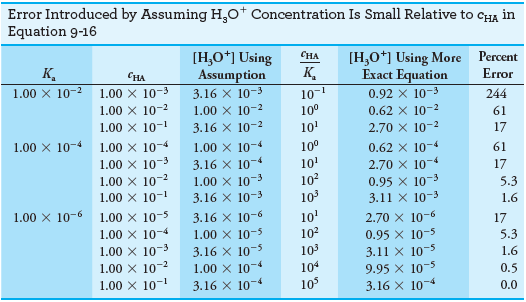
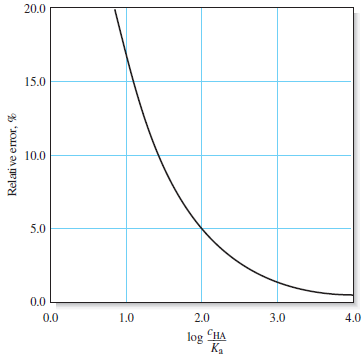
– The following table shows that the error introduced by the assumption that [H3O+] << cHA increases as the molar concentration of acid becomes smaller and its dissociation constant becomes larger.
– Notice that the error introduced by the assumption is about 0.5% when the ratio cHA/Kais 104.
– The error increases to about 1.6% when the ratio is 103, to about 5% when it is 102, and to about 17% when it is 10.
– The Following figure (1) illustrates the effect graphically.
– Notice that the hydronium ion concentration computed with the approximation becomes greater than or equal to the molar concentration of the acid when the ratio is less than or equal to 1, which is not meaningful.
– In general, it is a good idea to make the simplifying assumption and calculate a trial value for [H3O+] that can be compared with cHA in Equation (4).
– If the trial value alters [HA] by an amount smaller than the allowable error in the calculation, we consider the solution satisfactory.
– Otherwise, the quadratic equation must be solved to find a better value for [H3O+].
Solved problem (2) on Dissociation Constants
Calculate the hydronium ion concentration in 0.120 M nitrous acid.
Solution
– The principal equilibrium is:
– for which (see table below this subject ):
– Substitution into Equations (2) and (4) gives:
– When these relationships are introduced into the expression for Ka, we obtain:
– If we now assume that [H3O+] << 0.120, we find
– We now examine the assumption that 0.120 – 0.0092 ≈ 0.120 and see that the error is about 8%.
– The relative error in [H3O+] is actually smaller than this figure, however, as we can see by calculating log (cHA/Ka) = 2.2, which from Figure (1), suggests an error of about 4%.
– If a more accurate figure is needed, the quadratic equation gives an answer of 8.9 × 10-3 M for the hydronium ion concentration.
Solved problem (3) on Dissociation Constants
Calculate the hydronium ion concentration in a solution that is 2.0 × 10-4 M in aniline hydrochloride, C6H5NH3Cl.
Solution
– In aqueous solution, dissociation of the salt to Cl– and C6H5NH3+ is complete.
– The weak acid C6H5NH3+dissociates as follows:
– If we look in the table blow this subject, we find that the Kafor C6H5NH3+ is 2.51 × 10-5.
– Proceeding as in solved problem (2), we have
– Assume that [H3O+] << 2.0 × 10-4, and substitute the simplified value for [C6H5NH3+] into the dissociation-constant expression to obtain (see Equation 8)
– If we compare 7.09 × 10-5 with 2.0 × 10-4, we see that a significant error has been introduced by the assumption that [H3O+] << c C6H5NH3+(Figure (1|) indicates that this error is about 20%.)
– Thus, unless only an approximate value for [H3O+] is needed, it is necessary to use the more accurate expression (Equation 6)
– which rearranges to:
Hydronium Ion Concentration of Solutions of Weak Bases
– We can adapt the techniques of the previous sections to calculate the hydroxide or hydronium ion concentration in solutions of weak bases.
– Aqueous ammonia is basic as a result of the reaction:

– The predominant species in this solution is certainly NH3.
– Nevertheless, solutions of ammonia are still called ammonium hydroxide occasionally because at one time chemists thought that NH4OH rather than NH3 was the undissociated form of the base.
– We write the equilibrium constant for the reaction as:

Solved problem (4)
Calculate the hydroxide ion concentration of a 0.0750 M NH3 solution.
Solution
– The predominant equilibrium is:
– The chemical equation shows that:
– Both NH4+ and NH3 come from the 0.0750 M solution. Thus:
– If we substitute [OH–] for [ NH4+] in the second of these equations and rearrange, we find that:
– By substituting these quantities into the dissociation-constant, we have:
– which is analogous to Equation (4) for weak acids.
– If we assume that [OH–] << 7.50 × 10-2, this equation simplifies to:
– Comparing the calculated value for [OH–] with 7.50 × 10-2, we see that the error in [OH–] is less than 2%.
– If necessary, a better value for [OH–] can be obtained by solving the quadratic equation
Solved problem (5)
Calculate the hydroxide ion concentration in a 0.0100 M sodium hypochlorite solution.
Solution
– The equilibrium between OCl– and water is:

– The acid dissociation constant for HOCl from the table below in the subject is 3.0 × 10-8.
– Therefore, we rearrange Equation (1) and write:
– Proceeding as in solved problem (4), we have:
– In this case, we have assumed that [OH–] << 0.0100.
– We substitute this value into the equilibrium constant expression and calculate:
– Verify for yourself that the error resulting from the approximation is small.
Acid Dissociation Constants at 25 oC
Reference: Fundamentals of analytical chemistry / Douglas A. Skoog, Donald M. West, F. James Holler, Stanley R. Crouch. (ninth edition), 2014. USA