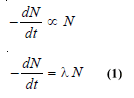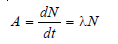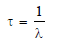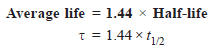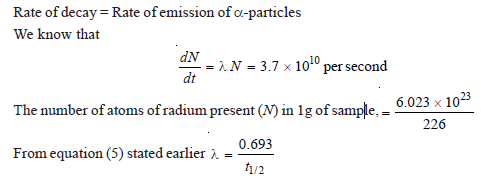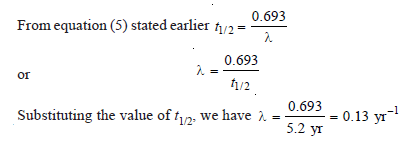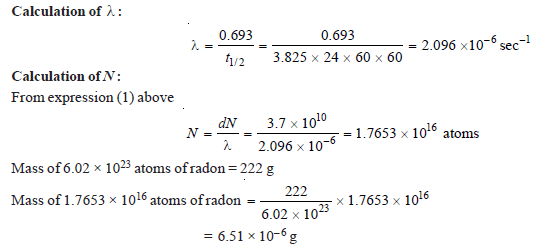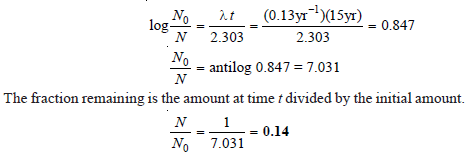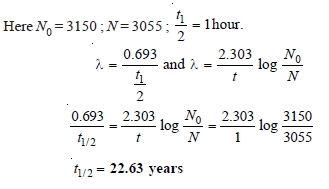Read Chemistry
– In this subject, we will discuss the Half-life time and radioactive decay: Equations, Calculations
Rate of radioactive decay
– The decay of a radioactive isotope takes place by disintegration of the atomic nucleus.
– It is not influenced by any external conditions.
– Therefore the rate of decay is characteristic of an isotope and depends only on the number of atoms present.
– If N is the number of undecayed atoms of an isotope present in a sample of the isotope, at time t,
– where – dN/dt means the rate of decrease in the number of radioactive atoms in the sample; and λ is the proportionality factor.
– This is known as the decay constant or disintegration constant.
– Putting dt = 1 in equation (1) we have:
– Thus decay constant may be defined as the proportion of atoms of an isotope decaying per second.
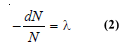
Units of Radioactivity
– The standard unit of radioactivity (i.e. rate of disintegration) is Curie (c).
– A curie is a quantity of radioactive material decaying at the same rate as 1 g of Radium (3.7 × 1010 dps).
– Rutherford is a more recent unit: 1 Rutherford = 106 dps
– The S.I. unit is Becquerel: 1 Bq = 1 dps
Half-Life time
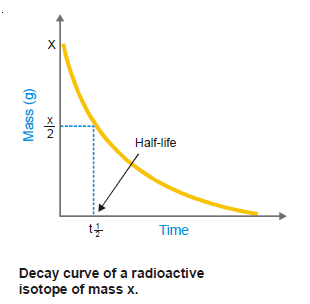
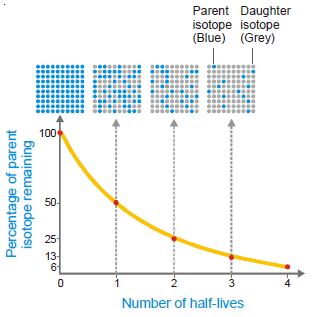
– The half-life or half-life period of a radioactive isotope is the time required for one-half of the isotope to decay.
– Or, it may be defined as the time for the radioactivity of an isotope to be reduced to half of its original value.
– The half-life period is characteristic of a radioactive element.
– For example, the half-life of radium is 1620 years.
– This means that 1g of radium will be reduced to 0.5 g in 1620 years and to 0.25 g in further 1620 years; and so on.
– Some other radioactive elements may have a half-life of a fraction of a second and for others, it may be millions of years.
– The unit of the half-life period is time– 1.
The activity of a Radioactive Substance
– It is defined as the rate of decay or the number of disintegrations per unit of time.
– The activity of a sample is denoted by A. It is given by the expression:
– The unit of activity is the curie (Ci) which is the rate of decay of 3.7 × 1010 disintegrations per second.
– The SI unit of activity is becquerel (Bq) which is defined as one disintegration per second.
– The activity of a radioactive sample is usually determined experimentally with the help of a Geiger-Muller counter.
Calculation of Half-Life time
– The value of λ can be found experimentally by finding the number of disintegrations per second with the help of a Geiger-Muller counter.
– Hence, the half-life of the isotope concerned can be calculated by using the relation (5).
Calculation of sample left after time T
– It follows from equation (4) stated earlier that
– Knowing the value of λ, the ratio of N0/N can be calculated.
– If the amount of the sample present to start with is given, the amount left after the lapse of time t can be calculated.
Average life
– In a radioactive substance, some atoms decay earlier and others survive longer.
– The statistical average of the lives of all atoms present at any time is called the Average life.
– It is denoted by the symbol τ and is the reciprocal of the decay constant, λ.
– The average life of a radioactive element is related to its half-life by the expression:
– The average life is often used to express the rate of disintegration of a radioactive element.
– So, The average life of radium is 2400 years.
Solved problem on Half-Life time
Problem (1)
Calculate the half-life of radium-226 if 1 g of it emits 3.7 × 1010 alpha particles per second.
Solution:
Problem (2)
Calculate the disintegration constant of cobalt 60 if its half-life to produce nickel–60 is 5.2 years.
Solution:
Problem (3)
The half-life period of radon is 3.825 days. Calculate the activity of radon. (atomic weight of radon = 222)
Solution:
– we know that:
dN = λN
– where dN is the number of atoms disintegrating per second, λ is the decay constant and N is the number of atoms in the sample of radon.
– By definition, the activity of radon is its mass in grams which gives 3.7 × 1010 disintegrations per second.
– Therefore activity of radon = 6.51 × 10– 6 g curie.
Problem (4)
Cobalt-60 disintegrates to give nickel-60. Calculate the fraction and the percentage of the sample that remains after 15 years. The disintegration constant of cobalt-60 is 0.13 yr– 1.
Solution:
– Hence the fraction remaining after 15 years is 0.14 or 14 percent of that present originally.
Problem (5)
How much time would it take for a sample of cobalt-60 to disintegrate to the extent that only 2.0 percent remains? The disintegration constant λ is 0.13 yr– 1.
Solution:
Problem (6)
A sample of radioactive 133 I gave with a Geiger counter of 3150 counts per minute at a certain time and 3055 counts per unit exactly after one hour later. Calculate the half-life period of 133I.
Solution:
Reference: Essentials of Physical Chemistry /Arun Bahl, B.S Bahl and G.D. Tuli / multicolor edition.
