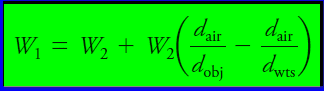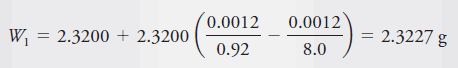Analytical Balance: Definition, Principle, Types, Examples
– In this subject, we will discuss the Analytical Balance: Definition, Principle, Types, Examples
– In most analyses, an analytical balance must be used to measure masses with high accuracy.
– Less accurate laboratory balances are also used for mass measurements when the demands for reliability are not critical.
What is An analytical balance?
– An analytical balance is an instrument for determining mass with a maximum capacity that ranges from 1 g to a few kilograms with a precision of at least 1 part in 105 at maximum capacity.
– The precision and accuracy of many modern analytical balances exceed 1 part in 106 at full capacity.
Types of Analytical Balances
(1) An analytical balance
– It has a maximum capacity that ranges from 1 g to several kilograms and precision at a maximum capacity of at least 1 part in 105.
(2) A microbalance
-It is the most common type of analytical balance, and it has a maximum load of 160 to 200 g and a precision of 0.1 mg.
(3) A semi-micro analytical balance
– It has a maximum load of 10 to 30 g and a precision of 0.01 mg.
(4) A microanalytical balance
– It has a maximum load of 1 to 3 g and a precision of 0.001 mg, or 1 μg.
– The most common analytical balances (macrobalances) have a maximum capacity ranging between 160 and 200 g.
– With these balances, measurements can be made with a standard deviation of +0.1 mg.
– Semimicroanalytical balances have a maximum loading of 10 to 30 g with a precision of +0.01 mg.
– A typical microanalytical balance has a capacity of 1 to 3 g and a precision of +0.001 mg (1 μg).
The analytical balance has evolved dramatically over the past several decades.
– The traditional analytical balance had two pans attached to either end of a lightweight beam that pivoted about a knife edge located in the center of the beam.
– The object to be weighed was placed on one pan.
– Standard masses were then added to the other pan to restore the beam to its original position.
– Weighing with such an equal-arm balance was tedious and time-consuming.
– The first single-pan analytical balance appeared on the market in 1946.
– The speed and convenience of weighing with this balance were vastly superior to what could be realized with the traditional equal-arm balance.
– As a result, this balance rapidly replaced the latter in most laboratories.
– The single-pan balance is currently being replaced by the electronic analytical balance, which has neither a beam nor a knife edge.
– The single-pan balance is still used in some laboratories, but the speed, ruggedness, convenience, accuracy, and capability for computer control and data logging of electronic balances ensure that the mechanical single-pan analytical balance will soon disappear from the scene.
Precautions in Using an Analytical Balance
– An analytical balance is a delicate instrument that you must handle with care.
– Consult with your instructor for detailed instructions on weighing with your particular model of balance.
– Observe the following general rules for working with an analytical balance regardless of make or model:
(1) Center the load on the pan as well as possible.
(2) Protect the balance from corrosion.
– Objects to be placed on the pan should be limited to nonreactive metals, nonreactive plastics, and vitreous, or glasslike, materials.
(3) Observe special precautions for the weighing of liquids.
(4) Consult your instructor if the balance appears to need adjustment.
(5) Keep the balance and its case scrupulously clean.
– A camel’s-hair brush is useful for removing spilled material or dust.
(6) Always allow an object that has been heated to return to room temperature before weighing it.
(7) Use tongs, finger pads, or a glassine paper strip to handle dried objects to prevent transferring moisture to them.
Sources of Error in Weighing by Analytical Balance
(1) Correction for Buoyancy
– A buoyancy error will affect data if the density of the object being weighed differs significantly from that of the standard masses.
– This error has its origin in the difference in buoyant force exerted by the medium (air) on the object and the masses.
– Buoyancy corrections for electronic balances may be accomplished with the equation:
- W1 = is the corrected mass of the object.
- W2 = the mass of the standard masses.
- dobj = the density of the object.
- dwts= the density of the masses.
- dair = the density of the air displaced by masses and objects.
– The value of dair is 0.0012 g/cm3.
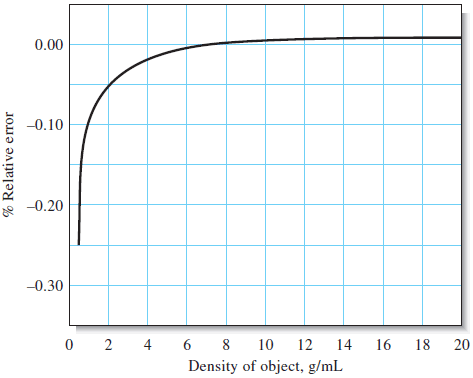
– The consequences of the Equation are shown in Figure blow in which the relative error due to buoyancy is plotted against the density of objects weighed in air against stainless steel masses.
– Note that this error is less than 0.1% for objects that have a density of 2 g/cm3 or greater.
– It is thus seldom necessary to correct the masses of most solids.
– The same cannot be said for low-density solids, liquids, or gases, however.
– For these, the effects of buoyancy are significant, and a correction must be applied.
– The density of masses used in single-pan balances (or to calibrate electronic balances) ranges from 7.8 to 8.4 g/cm3, depending on the manufacturer.
– The use of 8 g/cm3 is close enough for most purposes.
– If greater accuracy is required, the manufacturer’s specifications for the balance usually give the necessary density data.
Solved Problem
A bottle weighed 7.6500 g empty and 9.9700 g after the introduction of an organic liquid with a density of 0.92 g/cm3. The balance was equipped with stainless steel masses (d 8.0 g/cm3). Correct the mass of the sample for the effects of buoyancy.
Solution
– The apparent mass of the liquid is 9.9700 – 7.6500 = 2.3200 g.
– The same buoyant force acts on the container during both weighings.
– Thus, we need to consider only the force that acts on the 2.3200 g of liquid.
– By substituting 0.0012 g/cm3 for dair, 0.92 g/cm3 for dobj, and 8.0 g/cm3 for dwts in Equation above, we find that the corrected mass is:
(2) Temperature Effects
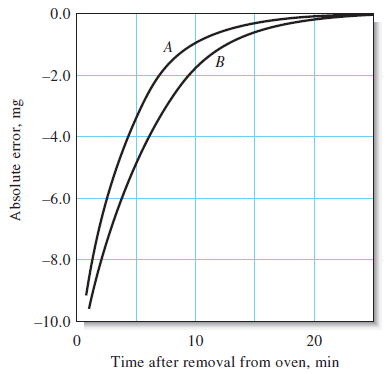
– Attempts to weigh an object whose temperature is different from that of its surroundings will result in a significant error.
– Failure to allow sufficient time for a heated object to return to room temperature is the most common source of this problem.
– Errors due to a temperature difference have two sources:
(a) convection currents within the balance case exert a buoyant effect on the pan and object.
(b) warm air trapped in a closed container weighs less than the same volume at a lower temperature.
– Both effects cause the apparent mass of the object to be low.
– This error can amount to as much as 10 or 15 mg for typical porcelain filtering crucibles or weighing bottles (see Figure ).
– Heated objects must always be cooled to room temperature before being weighed.
(3) Other Sources of Error
(a) A porcelain or glass object will occasionally acquire a static charge sufficient to cause a balance to perform erratically.
– This problem is particularly serious when the relative humidity is low.
– Spontaneous discharge frequently occurs after a short period.
(B) A low-level source of radioactivity (such as a Static-Master photographer’s brush containing a miniscule amount of polonium) in the balance case will ionize enough ions to neutralize the charge.
– Alternatively, the object can be wiped with a faintly damp chamois.
(C) The optical scale of a single-pan mechanical balance should be checked regularly for accuracy, particularly under loading conditions that require the full-scale range.
– A standard 100-mg mass is used for this check.
Reference: Fundamentals of analytical chemistry / Douglas A. Skoog, Donald M. West, F. James Holler, Stanley R. Crouch. (ninth edition), 2014. USA