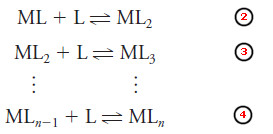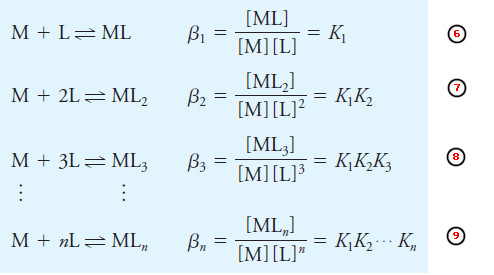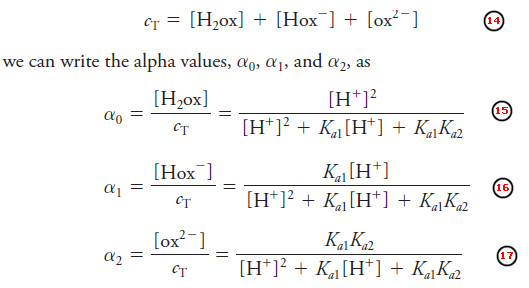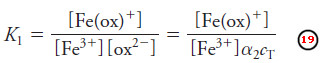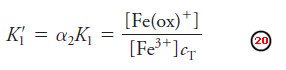The Formation of Complexes
The Formation of Complexes
– Most metal ions react with electron-pair donors to form coordination compounds or complexes.
– The donor species, or ligand, must have at least one pair of unshared electrons available for bond formation.
– Water, ammonia, and halide ions are common inorganic ligands. In fact most metal ions in aqueous solution actually exist as aquo complexes.
– Copper(II), for example, in aqueous solution is readily complexed by water molecules to form species such as Cu(H2O)42+.
– We often simplify such complexes in chemical equations by writing the metal ion as if it were uncomplexed Cu2+.
– We should remember, however, that most metal ions are actually aquo complexes in aqueous solution.
– The number of covalent bonds that a cation tends to form with electron donors is its coordination number.
– Typical values for coordination numbers are two, four, and six.
– The species formed as a result of coordination can be electrically positive, neutral, or negative.
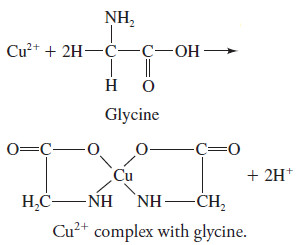
– For example, copper(II), which has a coordination number of four, forms a cationic ammine complex, Cu(NH3)42+; a neutral complex with glycine, Cu(NH2CH2COO)2; and an anionic complex with chloride ion, CuCl42-.
– Titrations based on complex formation, sometimes called complexometric titrations, have been used for more than a century.
– The truly remarkable growth in their analytical application, based on a particular class of coordination compounds called chelates, began in the 1940s.
– A chelate is produced when a metal ion coordinates with two or more donor groups of a single ligand to form a five- or six-membered heterocyclic ring.
– The copper complex of glycine, mentioned in the previous paragraph, is an example.
– In this complex, copper bonds to both the oxygen of the carboxyl group and the nitrogen of the amine group:
– A ligand that has a single donor group, such as ammonia, is called unidentate (single-toothed), whereas one such as glycine, which has two groups available for covalent bonding, is called bidentate.
– Tridentate, tetradentate, pentadentate, and hexadentate chelating agents are also known.
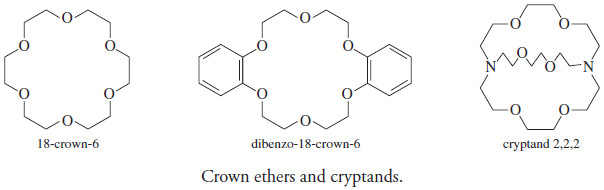
– Another important type of complex is formed between metal ions and cyclic organic compounds, known as macrocycles.
– These molecules contain nine or more atoms in the cycle and include at least three heteroatoms, usually oxygen, nitrogen or sulfur.
– Crown ethers, such as 18-crown-6 and dibenzo-18-crown-6 are examples of organic macrocycles.
– Some macrocyclic compounds form three dimensional cavities that can just accommodate appropriately sized metal ions.
– Ligands known as cryptands are examples.
– Selectivity occurs to a large extent because of the size and shape of the cycle or cavity relative to that of the metal ion, although the nature of the heteroatoms and their electron densities, the compatibility of the donor atoms with the metal ion, and several other factors also play important roles.
Complexation Equilibria
– Complexation reactions involve a metal-ion M reacting with a ligand L to form a complex ML, as shown in Equation (1):
– where we have omitted the charges on the ions in order to be general.
– Complexation reactions occur in a stepwise fashion and the reaction above is often followed by additional reactions:
– Unidentate ligands invariably add in a series of steps as shown above.
– With multidentate ligands, the maximum coordination number of the cation may be satisfied with only one or a few added ligands.
– For example, Cu(II), with a maximum coordination number of 4, can form complexes with ammonia that have the formulas Cu(NH3)2+, Cu(NH3)22+, Cu(NH3)32+, and Cu(NH3)42+.
– With the bidentate ligand glycine (gly), the only complexes that form are Cu(gly)2+ and Cu(gly)22+.
– The equilibrium constants for complex formation reactions are generally written as formation constants.
– Thus, each of the reactions (1) through (4) is associated with a stepwise formation constant K1 through K4.
– For example, K1 = [ML]/[M][L], K2 = [ML2]/[ML][L], and so on.
– We can also write the equilibria as the sum of individual steps.
– These have overall formation constants designated by the symbol βn. Therefore,
– Except for the first step, the overall formation constants are products of the stepwise formation constants for the individual steps leading to the product.
– For a given species like the free metal M, we can calculate an alpha value, which is the fraction of the total metal concentration in that form.
– Thus, αM is the fraction of the total metal present at equilibrium in the free metal form, αML is the fraction in the ML form, and so on.
– The alpha values are given by
– Note that these expressions are analogous to the a expressions we wrote for polyfunctional acids and bases except that the equations here are written in terms of formation equilibria while those for acids or bases are written in terms of dissociation equilibria.
– Also, the master variable is the ligand concentration [L] instead of the hydronium ion concentration.
– The denominators are the same for each a value.
– Plots of the α values versus p[L] are known as distribution diagrams.
The Formation of Insoluble Species of Complexes
– In the cases discussed in the previous section, the complexes formed are soluble in solution.
– The addition of ligands to a metal ion, however, may result in insoluble species, such as the familiar nickel-dimethylglyoxime precipitate.
– In many cases, the intermediate uncharged complexes in the stepwise formation scheme may be sparingly soluble, whereas the addition of more ligand molecules may result in soluble species.
– For example, adding Cl– to Ag+ results in the insoluble AgCl precipitate.
– Addition of a large excess of Cl– produces soluble species AgCl2–, AgCl32-, and AgCl43-.
– In contrast to complexation equilibria, which are most often treated as formation reactions, solubility equilibria are normally treated as dissociation reactions.
– In general, for a sparingly soluble salt MxAy in a saturated solution, we can write:
where Ksp is the solubility product.
– Hence, for BiI3, the solubility product is written, Ksp = [Bi3+][I–]3.
– The formation of soluble complexes can be used to control the concentration of free metal ions in solution and thus control their reactivity.
– For example, we can prevent a metal ion from precipitating or taking part in another reaction by forming a stable complex, which decreases the free metal-ion concentration.
– The control of solubility by complex formation is also used to achieve the separation of one metal ion from another.
– If the ligand is capable of protonation, as discussed in the next section, even more control can be accomplished by a combination of complexation and pH adjustment.
Ligands That Can Protonate
– Complexation equilibria can be complicated by side reactions involving the metal or the ligand.
– Such side reactions make it possible to exert some additional control over the complexes that form.
Metals can form complexes with ligands other than the one of interest.
– If these complexes are strong, we can effectively prevent complexation with the ligand of interest. Ligands can also undergo side reactions.
– One of the most common side reactions is that of a ligand that can protonate, that is, the ligand is a weak acid or the conjugate base of a weak acid.
Complexation with Protonating Ligands
– Consider the case of the formation of soluble complexes between the metal M and the ligand L, where the ligand L is the conjugate base of a polyprotic acid and forms HL, H2L, . . . HnL for which again the charges have been omitted for generality.
– Adding acid to a solution containing M and L reduces the concentration of free L available to complex with M and thus decreases the effectiveness of L as a complexing agent (Le Chatelier’s principle).
– For example, ferric ions (Fe3+) form complexes with oxalate (C2O42-, which we abbreviate as ox2-) with formulas [Fe(ox)]+, [Fe(ox)2]–, and [Fe(ox)3]3-. Oxalate can protonate to form Hox– and H2ox.
In basic solution, where most of the oxalate is present as ox2- before complexation with Fe3+, the ferric/oxalate complexes are very stable.
– Adding acid, however, protonates the oxalate ion, which in turn causes dissociation of the ferric complexes.
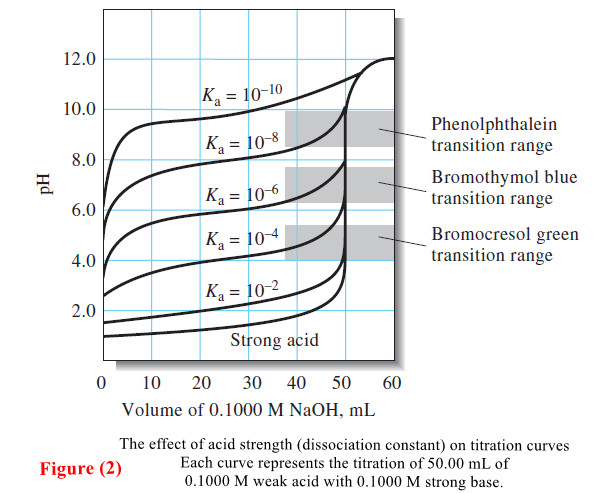
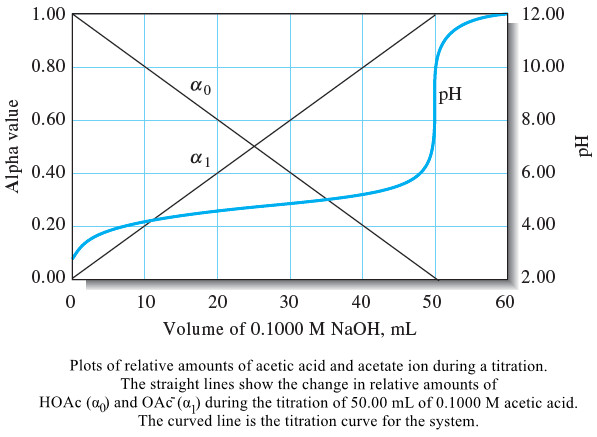
– For a diprotic acid, like oxalic acid, the fraction of the total oxalate-containing species in any given form, ox2-, Hox–, and H2ox, is given by an alpha value. Since
– Since we are interested in the free oxalate concentration, we will be most concerned with the highest a value, here α2.
– From Equation (17), we can write:
– Note that, as the solution gets more acidic, the first two terms in the denominator of Equation (17) dominate, and α2 and the free oxalate concentration decrease.
– When the solution is very basic, the last term dominates, α2 becomes nearly unity, and [ox2-] ≈ cT, indicating that nearly all the oxalate is in the ox2- form in basic solution.
Conditional Formation Constants
– To take into account the effect of pH on the free ligand concentration in a complexation reaction, it is useful to introduce a conditional formation constant, or effective formation constant.
– Such constants are pH-dependent equilibrium constants that apply at a single pH only.
– For the reaction of Fe3+ with oxalate, for example, we can write the formation constant K1 for the first complex as
– At a particular pH value, α2 is constant, and we can combine K1 and α2 to yield a new conditional constant K1‘:
– The use of conditional constants greatly simplifies calculations because cT is often known or is easily computed, but the free ligand concentration is not as easily determined.
– The overall formation constants, β values, for the higher complexes, [Fe(ox)2]– and [Fe(ox)3]3-, can also be written as conditional constants.
Reference
- Modern analytical chemistry / David Harvey / The McGraw-Hill Companies, Inc./ , 2000 . USA
- Dean’s Analytical Chemistry Handbook / Pradyot Patnaik / The McGraw-Hill Companies, 2nd Editionm, 2004 .USA
- Fundamentals of analytical chemistry / Douglas A. Skoog, Donald M. West, F. James Holler, Stanley R. Crouch. (ninth edition) , 2014 . USA