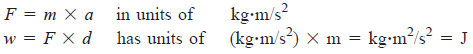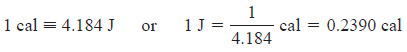Forms of Energy and Their Interconversion
Forms of Energy and Their Interconversion
– we discussed before the facts that all energy is either potential or kinetic and that these forms are convertible from one to the other.
– An object has potential energy by virtue of its position and kinetic energy by virtue of its motion.
– The potential energy of a weight raised above the ground is converted to kinetic energy as it falls.
– When the weight hits the ground, it transfers some of that kinetic energy to the soil and pebbles, causing them to move, and thereby doing work.
– In addition, some of the transferred kinetic energy appears as heat, as it slightly warms the soil and pebbles. Thus, the potential energy of the weight is converted to kinetic energy, which is transferred to the ground as work and as heat.
– Modern atomic theory allows us to consider other forms of energy—solar, electrical, nuclear, and chemical—as examples of potential and kinetic energy on the atomic and molecular scales.
– No matter what the details of the situation, when energy is transferred from one object to another, it appears as work and/or as heat.
– In this subject, we examine this idea in terms of the loss or gain of energy that takes place during a chemical or physical change.
The System and Its Surroundings
– In order to observe and measure a change in energy, we must first define the system, the part of the universe that we are going to focus on.
– The moment we define the system, everything else relevant to the change is defined as the surroundings.
– For example, in a flask containing a solution, if we define the system as the contents of the flask, then the flask itself, other nearby equipment, and perhaps the rest of the laboratory are the surroundings.
– In principle, the rest of the universe is the surroundings, but in practice, we need to consider only the portions of the universe relevant to the system.
– That is, it’s not likely that a thunderstorm in central Asia or a methane blizzard on Neptune will affect the contents of the flask, but the temperature, pressure, and humidity of the lab might.
Energy Flow to and from a System
Each particle in a system has potential energy and kinetic energy, and the sum of these energies for all the particles in the system is the internal energy, E, of the system (some texts use the symbol U).
– When a chemical system changes from reactants to products and the products return to the starting temperature, the internal energy has changed.
– To determine this change, ΔE, we measure the difference between the system’s internal energy after the change (Efinal) and before the change (Einitial):
– where Δ (Greek delta) means “change (or difference) in.” Note especially that Δ refers to the final state of the system minus the initial state.
– Because the total energy must be conserved, a change in the energy of the system is always accompanied by an opposite change in the energy of the surroundings.
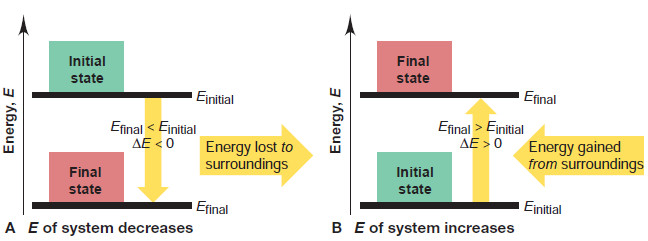
– We often represent this change with an energy diagram in which the final and initial states are horizontal lines on a vertical energy axis.
– The change in internal energy, ΔE, is the difference between the heights of the two lines.
– A system can change its internal energy in one of two ways:
(1) By losing some energy to the surroundings, as shown in Figure A:
(2) By gaining some energy from the surroundings, as shown in Figure B:
– Note that the change in energy is always an energy transfer from system to surroundings, or vice versa.
Heat and Work: Two Forms of Energy Transfer
– Just as we saw when a weight hits the ground, energy transfer outward from the system or inward from the surroundings can appear in two forms, heat and work.
– Heat (or thermal energy, symbol q) is the energy transferred between a system and its surroundings as a result of a difference in their temperatures only.
– Energy in the form of heat is transferred from hot soup (system) to the bowl, air, and table (surroundings) because the surroundings have a lower temperature.
– All other forms of energy transfer (mechanical, electrical, and so on) involve some type of work (w), the energy transferred when an object is moved by a force.
– When you (system) kick a football (surroundings), energy is transferred as work to move the ball.
– When you inflate the ball, the inside air (system) exerts a force on the inner wall of the ball (surroundings) and does work to move it outward.
– The total change in a system’s internal energy is the sum of the energy transferred as heat and/or work:
– The numerical values of q and w (and thus ΔE) can be either positive or negative, depending on the change the system undergoes.
– In other words, we define the sign of the energy transfer from the system’s perspective. Energy coming into the system is positive.
– Energy going out from the system is negative.
– Of the innumerable changes possible in the system’s internal energy, we’ll examine the four simplest—two that involve only heat and two that involve only work.
Energy Transfer as Heat Only
– For a system that does no work but transfers energy only as heat (q), we know that w = 0.
– Therefore, from Equation 2, we have ΔE = q + 0 = q.
– There are two possibilities:
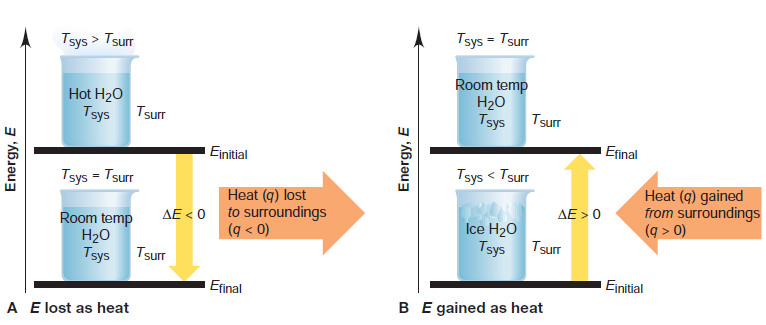
(1) Heat flowing out from a system
– Suppose a sample of hot water is the system; then, the beaker containing it and the rest of the lab are the surroundings.
– The water transfers energy as heat to the surroundings until the temperature of the water equals that of the surroundings.
– The system’s energy decreases as heat flows out from the system, so the final energy of the system is less than its initial energy.
– Heat was lost by the system, so q is negative, and therefore ΔE is negative (Figure A).
(2) Heat flowing into a system
– If the system consists of ice water, it gains energy as heat from the surroundings until the temperature of the water equals that of the surroundings.
– In this case, energy is transferred into the system, so the final energy of the system is higher than its initial energy.
– Heat was gained by the system, so q is positive, and therefore ΔE is positive (Figure B).
Energy Transfer as Work Only
– For a system that transfers energy only as work (w), q = 0; therefore, ΔE = 0 + w = w.
– Once again, there are two possibilities:
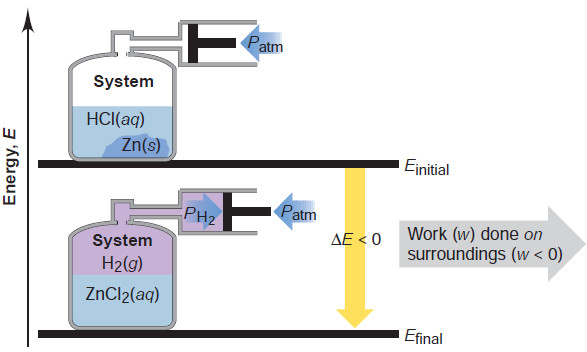
1. Work done by a system
– Consider the reaction between zinc and hydrochloric acid as it takes place in an insulated container attached to a piston-cylinder assembly.
– We define the system as the atoms that make up the substances.
– In the initial state, the system’s internal energy is that of the atoms in the form of the reactants, metallic Zn and aqueous H+ and Cl– ions.
– In the final state, the system’s internal energy is that of the same atoms in the form of the products, H2 gas and aqueous Zn2+ and Cl– ions:
Zn(s) + 2H+(aq) + 2Cl–(aq) → H2(g) → Zn2+(aq) + 2Cl–(aq)
– As the H2 gas forms, some of the internal energy is used by the system to do work on the surroundings and push the piston outward.
– Energy is lost by the system as work, so w is negative and ΔE is negative, as you see in Figure.
– The H2 gas is doing pressure-volume work (PV work), the type of work in which a volume changes against an external pressure.
– The work done here is not very useful because it simply pushes back the piston and outside air.
– But, if the system is a ton of burning coal and O2, and the surroundings are a locomotive engine, much of the internal energy lost from the system does the work of moving a train.
2. Work done on a system.
– If we increase the external pressure on the piston in Figure , the system gains energy because work is done on the system by the surroundings: w is positive, so ΔE is positive.
– The Table summarizes the sign conventions for q and w and their effect on the sign of ΔE.
The Law of Energy Conservation
– As you’ve seen, when a system gains energy, the surroundings lose it, and when a system loses energy, the surroundings gain it.
– Energy can be converted from one form to another as these transfers take place, but it cannot simply appear or disappear—it cannot be created or destroyed.
– The law of conservation of energy restates this basic observation as follows: the total energy of the universe is constant.
– This law is also known as the first law of thermodynamics.
– Conservation of energy applies everywhere. As gasoline burns in a car engine, the released energy appears as an equivalent amount of heat and work.
– The heat warms the car parts, passenger compartment, and surrounding air.
– The work appears as mechanical energy to turn the car’s wheels and belts.
– That energy is converted further into the electrical energy of the clock and radio, the radiant energy of the headlights, the chemical energy of the battery, the heat due to friction, and so forth.
– If you took the sum of all these energy forms, you would find that it equals the change in energy between the reactants and products as the gasoline is burned.
– Complex biological processes also obey conservation of energy.
– Through photosynthesis, green plants convert radiant energy from the Sun into chemical energy, transforming low-energy CO2 and H2O into high-energy carbohydrates (such as wood) and O2.
– When the wood is burned in air, those low-energy compounds form again, and the energy difference is released to the surroundings.
– Thus, energy transfers between system and surroundings can be in the forms of heat and/or various types of work—mechanical, electrical, radiant, chemical— but the energy of the system plus the energy of the surroundings remains constant: energy is conserved.
– A mathematical expression of the law of conservation of energy (first law of thermodynamics) is:
– This profound idea pertains to all systems, from a burning match to the movement of continents, from the inner workings of your heart to the formation of the Solar System.
Units of Energy
– The SI unit of energy is the joule (J), a derived unit composed of three base units:
– Both heat and work are expressed in joules. Let’s see how these units arise in the case of work.
– The work (w) done on a mass is the force (F) times the distance (d) that the mass moves:
w = F × d
– A force changes the velocity of (accelerates) a mass.
– Velocity has units of meters per second (m/s), so acceleration(a) has units of m/s2.
– Force, therefore, has units of mass (m, in kilograms) times acceleration:
– Potential energy, kinetic energy, and PV work are combinations of the same physical quantities and are also expressed in joules.
– The calorie (cal) is an older unit that was defined originally as the quantity of energy needed to raise the temperature of 1 g of water by 1°C (from 14.5°C to 15.5°C).
– The calorie is now defined in terms of the joule.
– Because the quantities of energy involved in chemical reactions are usually quite large, chemists use the unit the kilojoule (kJ), or sometimes the kilocalorie (kcal):
– The nutritional Calorie (note the capital C), the unit used to measure the energy available from food, is actually a kilocalorie.
– The British thermal unit (Btu), a unit in engineering that you may have seen used to indicate energy output of appliances, is the quantity of energy required to raise the temperature of 1 lb of water by 1°F and is equivalent to 1055 J.
– In general, the SI unit (J or kJ) is used throughout this text.
State Functions and the Path Independence of the Energy Change
– An important point to understand is that there is no particular sequence by which the internal energy (E) of a system must change.
– This is because E is a state function, a property dependent only on the current state of the system (its composition volume, pressure, and temperature), not on the path the system took to reach that state; the current state depends only on the difference between the final and initial states.
– Thus, the energy change of a system can occur by any one of countless combinations of heat (q) and work (w).
– No matter what the combination, however, the same overall energy change occurs, because ΔE does not depend on how the change takes place.
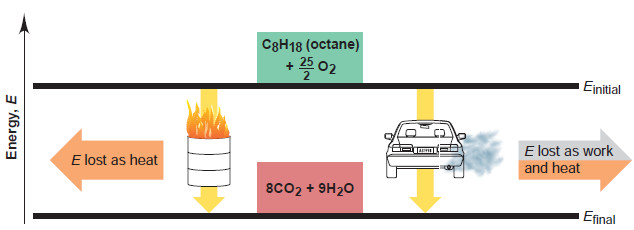
– As an example, let’s define a system in its initial state as 1 mol of octane (a component of gasoline) together with enough O2 to burn it.
– In its final state, the system is the CO2 and H2O that form (a fractional coefficient is needed for O2 because we specified 1 mol of octane):
– Energy is released to warm the surroundings and/or do work on them, so ΔE is negative.
– Two of the ways the change can occur are shown in Figure.
– If we burn the octane in an open container, ΔE appears almost completely as heat (with a small amount of work done to push back the atmosphere).
– If we burn it in a car engine, a much larger portion (≈30%) of ΔE appears as work that moves the car, with the rest used to heat the car, exhaust gases, and surrounding air.
– And If we burn the octane in a lawn mower or a plane, ΔE appears as other combinations of work and heat.
– Thus, for a given change, ΔE (sum of q and w) is constant, even though q and w can vary.
– Heat and work are not state functions because their values do depend on the path the system takes in undergoing the energy change.
– The pressure (P) of an ideal gas or the volume (V) of water in a beaker are other examples of state functions.
– This path independence means that changes in state functions—ΔE, ΔP, and ΔV—depend only on their initial and final states.
– (Note that symbols for state functions, such as E, P, and V, are capitalized.)
SUMMARY: Forms of Energy and Their Interconversion
– Energy is transferred as heat (q) when the system and surroundings are at different temperatures; energy is transferred as work (w) when an object is moved by a force.
– Heat or work gained by a system (q > 0; w> 0) increases its internal energy (E); heat or work lost by the system (q < 0; w < 0) decreases E.
– The total change in the system’s internal energy is the sum of the heat and work: ΔE = q + w.
– Heat and work are measured in joules (J).
– Energy is always conserved: it changes from one form into another, moving into or out of the system, but the total quantity of energy in the universe (system plus surroundings) is constant.
– Energy is a state function, which means that the same ΔE can occur through any combination of q and w.
References
- Principles of Inorganic Chemistry / Brian W. Pfennig / 1st ed, 2015 /John Wiley & Sons, Inc/ USA.
- Principles of general Chemistry / Martin S. Silberberg / 2nd ed, 2010 /The McGraw-Hill Companies, Inc./ USA.
- Inorganic Chemistry /Peter Atkins, Tina Overton, Jonathan Rourkel, Mark Weller, Fraser Armstrong, Mike Hagerman / 6th ed, 2014 /W. H. Freeman and Company/ New York, USA.
-
